Does A Suppressor Change Point Of Impact
This post compares a few change point detection method available in R given different time series dynamics and inquiry questions. Modify points or breakpoints are abrupt variations in time series data and may represent transitions between dissimilar states. The detection of modify points is useful in modelling and prediction of time series and is found in application areas such every bit medical condition monitoring, speech and image analysis or climate change detection. In marine ecology, such analysis is oft applied to place sudden shifts in single populations or entire communities and environmental conditions1. In this case, the change points detection algorithms are applied to single time serial and the change points correspond simply breaks in time.
More than recently, the presence and location of change points (then often termed thresholds) is studied in ecosystem indicators to ameliorate interpret and foresee impacts of changes in the intensities of human and environmental pressures2. But here, the focus is more on modify signal in the relationship betwixt a response (i.e. indicator) and explanatory (pressure) variable. But which detection method should be used for this case? I ran into this outcome when analyzing indicator-pressure relationships and potential modify points for the Baltic Bounding main. So I started to compare some of the commonly used algorithms by using bogus time series information for which I knew the exact number and location or functional response curve. I thought it might be nice to share the outcome with you lot and the decision I drew from the comparison. I won't get into too much detail about each package'southward role and their settings simply I volition try to explain a fleck more including the R code in the first, existent dataset. Subsequently that I will only show the numerical and graphical output to be not as well lengthy!
R packages for detecting change points
The following packages available on CRAN will be compared:
-
changepoint: changes in mean and variance of fourth dimension series -
bcp: changes in mean; Bayesian approach -
strucchange: changes in (time series) regression model -
segmented: changes in regression (does not have to exist time serial data) -
tree: classification or regression tree
The changepoint packet provides many methods for performing change bespeak analysis of univariate fourth dimension series3. Although the packet only considers the case of independent observations, the theory behind the implemented methods allows for certain types of serial dependence. For specific methods, the expected computational cost tin be shown to be linear with respect to the length of the time serial. Currently, the changepoint package is only suitable for finding changes in hateful or variance. This package also estimates multiple change points through the use of penalty. The drawback to this arroyo is that it requires a user specified penalisation term. A prissy tutorial by Rebecca Killick tin can be found here. The core office I volition use here is cpt.hateful() with
- the default AMOC method for single changepoint detection
- the PELT method for detecting multiple changepoints setting the penalty type to AIC and CROPS
The bcp package is designed to perform Bayesian unmarried modify signal analysis of univariate fourth dimension serial4. It returns the posterior probability of a change betoken occurring at each time index in the series. Contempo versions of this package have reduced the computational cost from quadratic to linear with respect to the length of the series. However, all versions of this package are merely designed to detect changes in the mean of contained Gaussian observations with its core function bcp().
The strucchange package provides a suite of tools for detecting changes within linear regression modelsfive. Many of these tools however, focus on detecting at near one modify inside the regression model. This bundle also contains methods that perform online change detection, thus allowing it to be used in settings where there are multiple changes. Additionally, if the number of changes is known a priori and so the breakpoint method can be used to perform retrospective assay. For a given number of changes, this method returns the change point estimates which minimizes the residuum sum of squares. There are 3 approaches I will use here:
- tests from the generalized fluctuation test (GFT) framework that can observe various types of structural changes:
efp()andsctest() - test from the F test framework, which assume that there is one (un- known) breakpoint:
Fstats() - examination for simultaneous estimation of multiple breakpoints in time serial regression models:
breakpoints()→ here one cane specify in the formula whether one wants to test for a change in the mean (i.e. the intercept) or in the relationship to an explanatory variable.
The segmented package provides functions for segmented or broken-line models, which are regression models where the relationships between the response and one or more explanatory variables are piecewise linear, namely represented by two or more straight lines connected at specific breakpoints6. The number of breakpoints of each segmented relationship must exist a priori specified.
An culling arroyo are so-chosen decision trees. These tree-based methods for regression and classification involve stratifying or segmenting the predictor space into a number of unproblematic regions. The value at which the regions are dissever tin can too be seen as change points in the predictor. While there are numerous tree methods (e.g. boosting, bagging, random forest) and implementations in R I will here apply the unproblematic unmarried conclusion tree arroyo that is provided by the tree package.
This list of change point detection methods is surely not exclusive just represents fairly well the methods that have been commonly used to analyze ecological regime shifts in marine systems.
Summary
I will outset right with the synthesis of my comparison so you can skip the fourth dimension- and method-specific outcomes. The list of individual results y'all'll find below is actually pretty long as I compare 8 methods on 6 dissimilar fourth dimension series (the first is the internal Nile dataset the others are artificial/ simulated datasets). So to spare yous all these tedious plots and numeric outputs I summarized here all results into i table and a few figures.
I will start correct with the synthesis of my comparison and so you can skip the slow and lengthy outcomes of 8 methods that I test on 1 existent and 5 artificial information sets. Here is an overview table that shows for each method and dataset the location of each detected change points.
| Fourth dimension series (loc of truthful cpts) | AMOC | PELT-AIC | PELT-CROPS | bcp | GFT (F test) | Breakpoints | segmented | tree |
| 1 change in hateful (Nile data, #28) | 28 | (besides many) | (besides many) | 28 | 28 | 28 | 3 | 28 |
| 1 change in hateful (at #25) | 25 | 25 | 13,14,23,24,25 | 25 | 25 | 25 | 14 | 25 |
| iii changes in mean (at #10,25,45) | none | x,26,46 | ten,26,46 | 26 | 26 | x,26,34 | 20 | 10,xvi,26,33,45 |
| i intermission in human relationship (at #10) | 6 | 3,8,13,18 | 3,8,13,eighteen | eight | 8 (6) | 10 | eleven | 6,xiv |
| Cubic decay part | 35 | (likewise many) | none | 32,43 | 30 (34) | 8,26,41 | xxx | 25,35,43 |
| Highly non-linear (four breaks at #10,25,45) | none | 17,32 | 17,31,39,45 | 39,45 | 33 (39) | x,26,43 | 11,26,44 | 16,22,32,39,45 |
Have home message
- Obviously there is no ane-method-fits-all!
- To detect the ane major changepoint in the time series several methods tin exist applied.
- But to notice the multiple existing changepoints in dataset iii but the PELT algorithm (contained of the penalisation blazon) performed well.
- The changepoints in the relationship betwixt two variables were only detected by the regression breakpoint and segmented algorithm.
- Particularly the
breakpoints()stands out equally it tin detect changepoints in means of single time series but also in functional response curves and it does not require any a priori conclusion of numbers of changepoints! - A practiced pick might be the complementary use of the PELT algorithm in the changepoint parcel with the breakpoints method in strucchange.
- If ane is interested to know when a response variable such as an ecosystem indicator starts to severely deteriorate due to the intensification of a item human or environmental pressure than regression-based method such equally breakpoints or segmented might exist a amend pick.
For a visual comparison of the better performing models all five artificial time series and the changes in the mean means or relationship are plotted here:
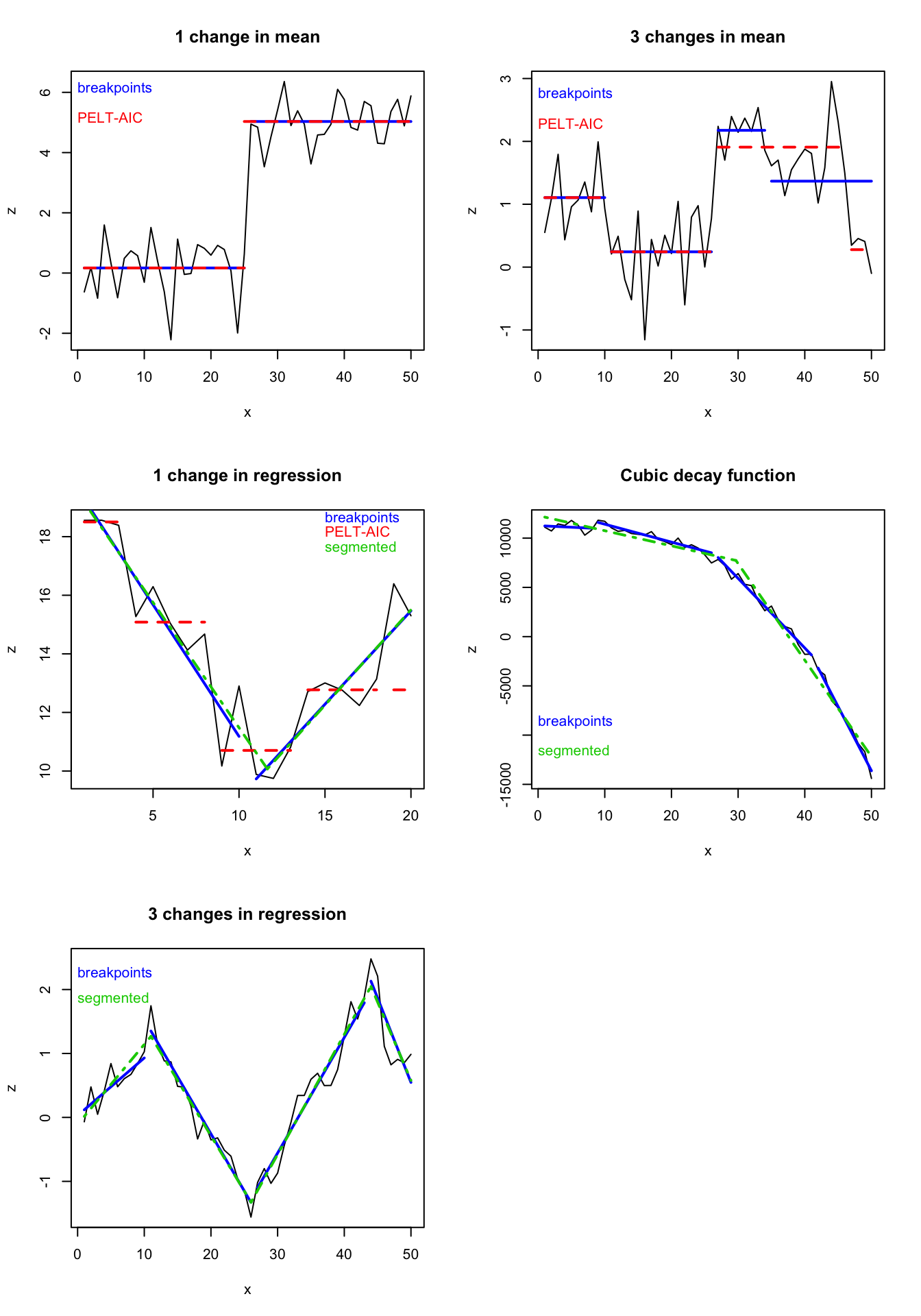
Pros and cons of each method
Changes in mean
-
changepoint:- disadvantage here is that one needs to specify a priori if ane or multiple changes and
- in that location are many parameters to ready which can lead to dissimilar results
- when penalty set to "CROPS", one needs to visually inspect the optimal number of modify points
-
bcp:- easy to apply, not much to specify
- no specification of modify points to set a priori
- detection rate depends more than on the magnitude of change than other methods
-
strucchange:- can cope with many model types, likewise for changes in means by specifying y ~ ane
- provides confidence intervals of change points
- several examination statistics for checking for structural changes:
sctest(),Fstats(),breakpoints() - disav.: sum of the output is tuned to ts object, needs some recoding to suit to ordinary dataframe (→ applies to
sctest(),Fstats())
-
segmented: useless for changes in hateful! -
tree:- the method found all truthful changepoints
- simply unfortunately likewise some more than –> how to choose the optimal 1?
Changes in functional curves of relationships between X and Y
-
strucchange:- provides several test statistics
- no a priori specification of alter points
- provides confidence intervals around the location of the change points!
- allows different type of model structures (but that also requires the correct specification)
-
segmented:- disadv.: requires starting values for the change points, hence, one needs to decide the number of change points a priori
- adv.: provides too conviction intervals around the location of the change points!
- disadv.: very simple model structure only allowed
Detailed results and R code of detection operation under different scenarios
# Loading packages library(changepoint) library(bcp) library(strucchange) library(segmented) library(tree) 1 change in mean
Real data: Nile dataset
The Nile dataset comes with the R dataset package and represents measurements of the annual flow (in unit of measurement 108 m3) of the river Nile at Aswan, between 1871 and 1970. Effectually 1898, the annual menses dropped greatly from circa 1100 to 8007. We will test now whether this shift in 1898 (i.east. in year 28 of the time series) will be detected by all 5 methods.
information(Nile) str(Nile) ## Fourth dimension-Serial [1:100] from 1871 to 1970: 1120 1160 963 1210 1160 1160 813 1230 1370 1140 ... plot(Nile) 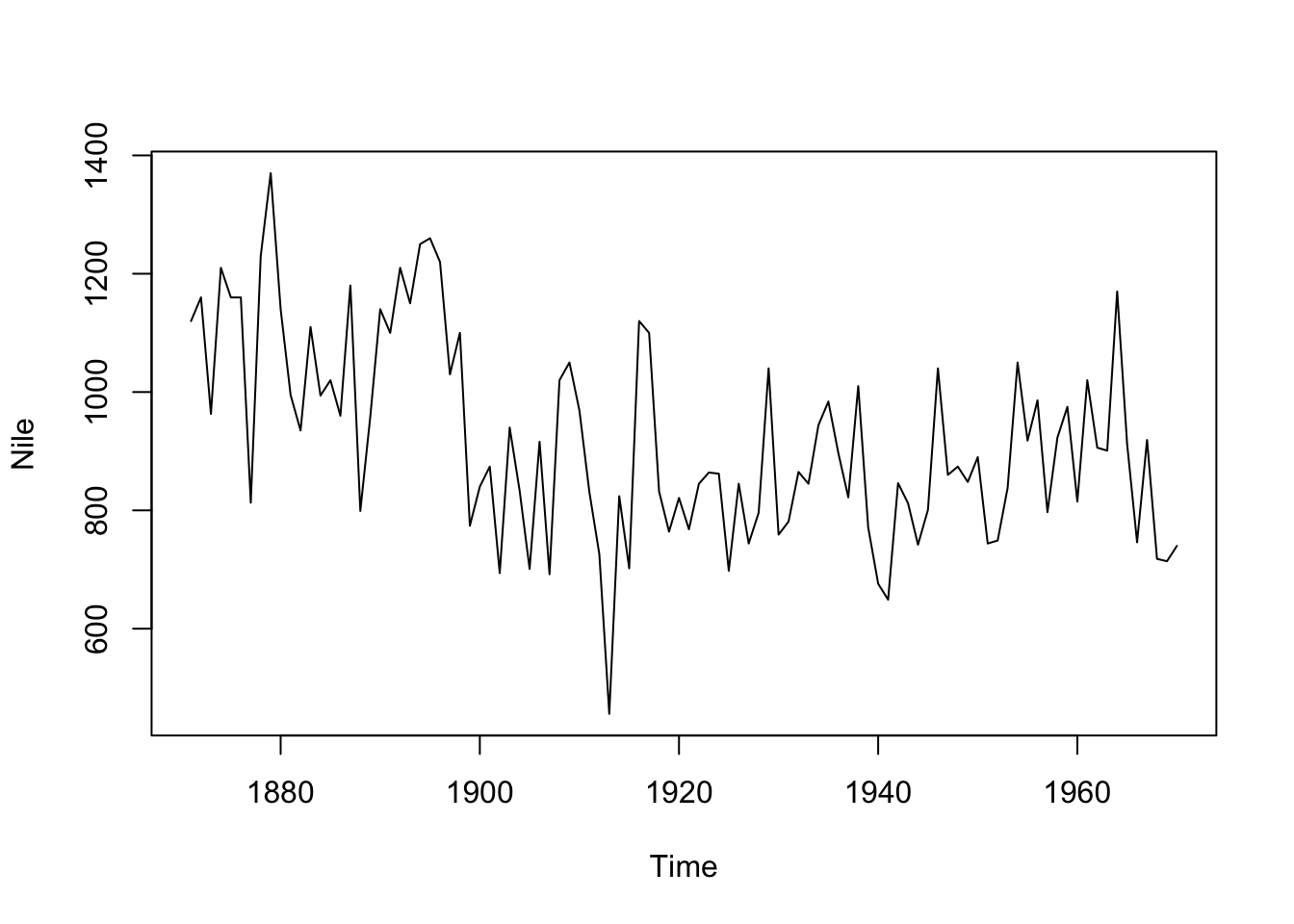
changepoint
Looking for 1 modify bespeak using the "AMOC" method (which is likewise the default):
cpt.mean(Nile, method = "AMOC") ## Class 'cpt' : Changepoint Object ## ~~ : S4 class containing 12 slots with names ## cpttype date version data.set method examination.stat pen.blazon pen.value minseglen cpts ncpts.max param.est ## ## Created on : Fri April 26 15:58:35 2019 ## ## summary(.) : ## ---------- ## Created Using changepoint version ii.2.ii ## Changepoint type : Change in mean ## Method of analysis : AMOC ## Exam Statistic : Normal ## Type of penalty : MBIC with value, 13.81551 ## Minimum Segment Length : i ## Maximum no. of cpts : 1 ## Changepoint Locations : 28 The method identifies correctly a alter betoken in 1898 (#28). What would happen when using the setting for identifying multiple modify points (if we wouldn't know the exact number):
cpt.hateful(Nile, method = "PELT", Q = 10) ## Grade 'cpt' : Changepoint Object ## ~~ : S4 course containing 12 slots with names ## cpttype engagement version data.set method test.stat pen.type pen.value minseglen cpts ncpts.max param.est ## ## Created on : Fri Apr 26 xv:58:35 2019 ## ## summary(.) : ## ---------- ## Created Using changepoint version ii.2.2 ## Changepoint type : Modify in mean ## Method of analysis : PELT ## Examination Statistic : Normal ## Type of punishment : MBIC with value, 13.81551 ## Minimum Segment Length : ane ## Maximum no. of cpts : Inf ## Number of changepoints: 94 cpt2 <- cpt.mean(Nile, method = "PELT", penalization = "CROPS", pen.value = c(1,25)) ## [1] "Maximum number of runs of algorithm = 6" ## [1] "Completed runs = 2" ## [1] "Completed runs = 3" ## [1] "Completed runs = 5" summary(cpt2) ## Created Using changepoint version two.two.ii ## Changepoint type : Alter in mean ## Method of assay : PELT ## Test Statistic : Normal ## Blazon of penalty : CROPS with value, i 25 ## Minimum Segment Length : 1 ## Maximum no. of cpts : Inf ## Changepoint Locations : ## Range of segmentations: ## [,1] [,ii] [,three] [,4] [,five] [,half-dozen] [,7] [,8] [,9] [,x] [,11] [,12] [,13] ## [1,] 1 2 3 4 vi 7 viii 9 x 11 12 13 xiv ## [2,] 1 2 three four 6 7 8 nine x 11 12 13 14 ## [3,] ane 2 3 iv six seven 8 nine 10 eleven 12 13 14 ## [4,] 1 two 3 4 6 7 8 9 ten 11 12 xiii 14 ## [,xiv] [,15] [,16] [,17] [,18] [,nineteen] [,20] [,21] [,22] [,23] [,24] ## [ane,] 15 xvi 17 eighteen 19 twenty 21 22 23 24 25 ## [2,] 15 xvi 17 18 xix 20 21 22 23 24 25 ## [3,] 15 16 17 xviii 19 20 21 22 23 24 25 ## [4,] 15 xvi 17 18 19 twenty 21 22 23 24 25 ## [,25] [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] ## [1,] 26 27 28 29 30 31 32 33 34 35 36 ## [2,] 26 27 28 29 xxx 31 32 33 34 35 36 ## [iii,] 26 27 28 29 30 31 32 33 34 35 36 ## [four,] 26 27 28 29 30 31 32 33 34 35 36 ## [,36] [,37] [,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] ## [1,] 37 38 39 40 41 42 43 44 45 46 47 ## [2,] 37 38 39 forty 41 42 43 44 45 46 47 ## [three,] 37 38 39 40 41 42 43 44 45 46 47 ## [4,] 37 38 39 twoscore 41 42 43 44 45 46 47 ## [,47] [,48] [,49] [,l] [,51] [,52] [,53] [,54] [,55] [,56] [,57] ## [one,] 48 49 50 51 52 53 54 55 56 57 58 ## [2,] 48 49 50 51 52 54 55 56 57 58 59 ## [three,] 48 49 l 51 52 54 55 56 57 58 59 ## [4,] 48 49 50 51 52 54 55 56 57 58 59 ## [,58] [,59] [,60] [,61] [,62] [,63] [,64] [,65] [,66] [,67] [,68] ## [1,] 59 lx 61 62 63 64 65 66 67 68 69 ## [2,] 60 61 62 63 64 65 66 67 68 69 70 ## [3,] sixty 61 62 63 64 65 66 67 68 69 70 ## [iv,] lx 61 62 63 64 65 66 67 68 69 lxx ## [,69] [,70] [,71] [,72] [,73] [,74] [,75] [,76] [,77] [,78] [,79] ## [1,] lxx 71 72 73 74 75 76 77 78 79 80 ## [2,] 71 72 73 74 75 76 77 78 79 80 81 ## [3,] 71 72 73 74 75 76 77 78 79 lxxx 81 ## [4,] 71 72 73 74 75 76 77 78 79 80 82 ## [,eighty] [,81] [,82] [,83] [,84] [,85] [,86] [,87] [,88] [,89] [,90] ## [1,] 81 82 83 84 85 86 87 88 89 90 91 ## [2,] 82 83 84 85 86 87 88 89 ninety 91 92 ## [3,] 82 83 84 85 86 87 88 89 90 91 92 ## [four,] 83 84 85 86 87 88 89 90 91 93 94 ## [,91] [,92] [,93] [,94] [,95] [,96] [,97] [,98] ## [1,] 92 93 94 95 96 97 98 99 ## [2,] 93 94 95 96 97 98 99 NA ## [three,] 93 94 95 96 97 99 NA NA ## [4,] 95 96 97 99 NA NA NA NA ## ## For penalty values: 1 two 8 12.five Nosotros can also plot the diagnostics to encounter the number of changepoints in each sectionalization confronting the change in examination statistic when adding that change. The plot is similar to the scree plot in principal component analysis every bit when a true changepoint is added the cost increases or decreases speedily, but when a changepoint due to noise is added the change is modest:
plot(cpt2, diagnostic = Truthful) 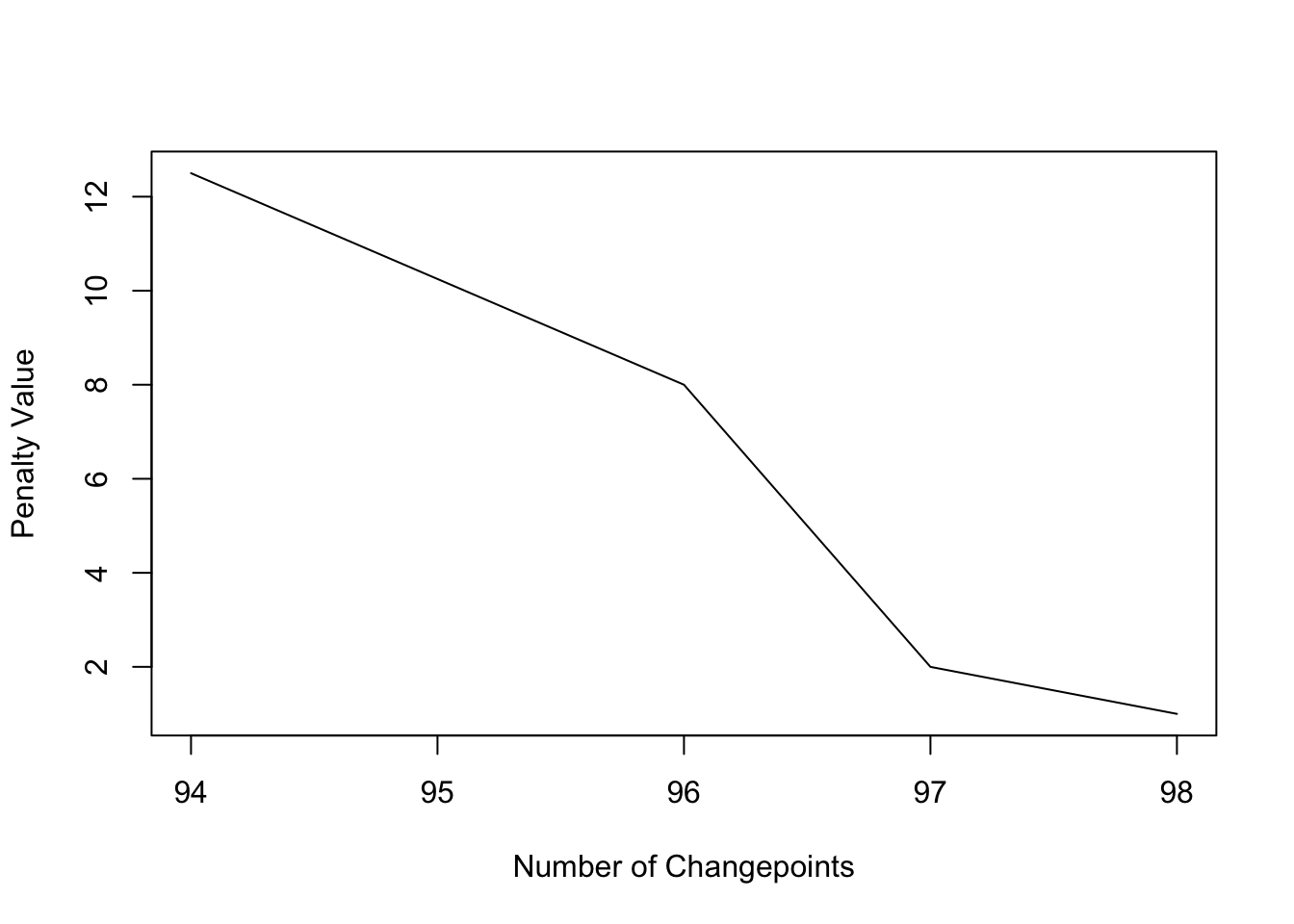
The PELT algorithm detects too many change points (aforementioned when methods "SegNeigh" or "BinSeg" were used).
bcp
x <- Nile bcp_x <- bcp(10, return.mcmc = Truthful) plot(bcp_x) 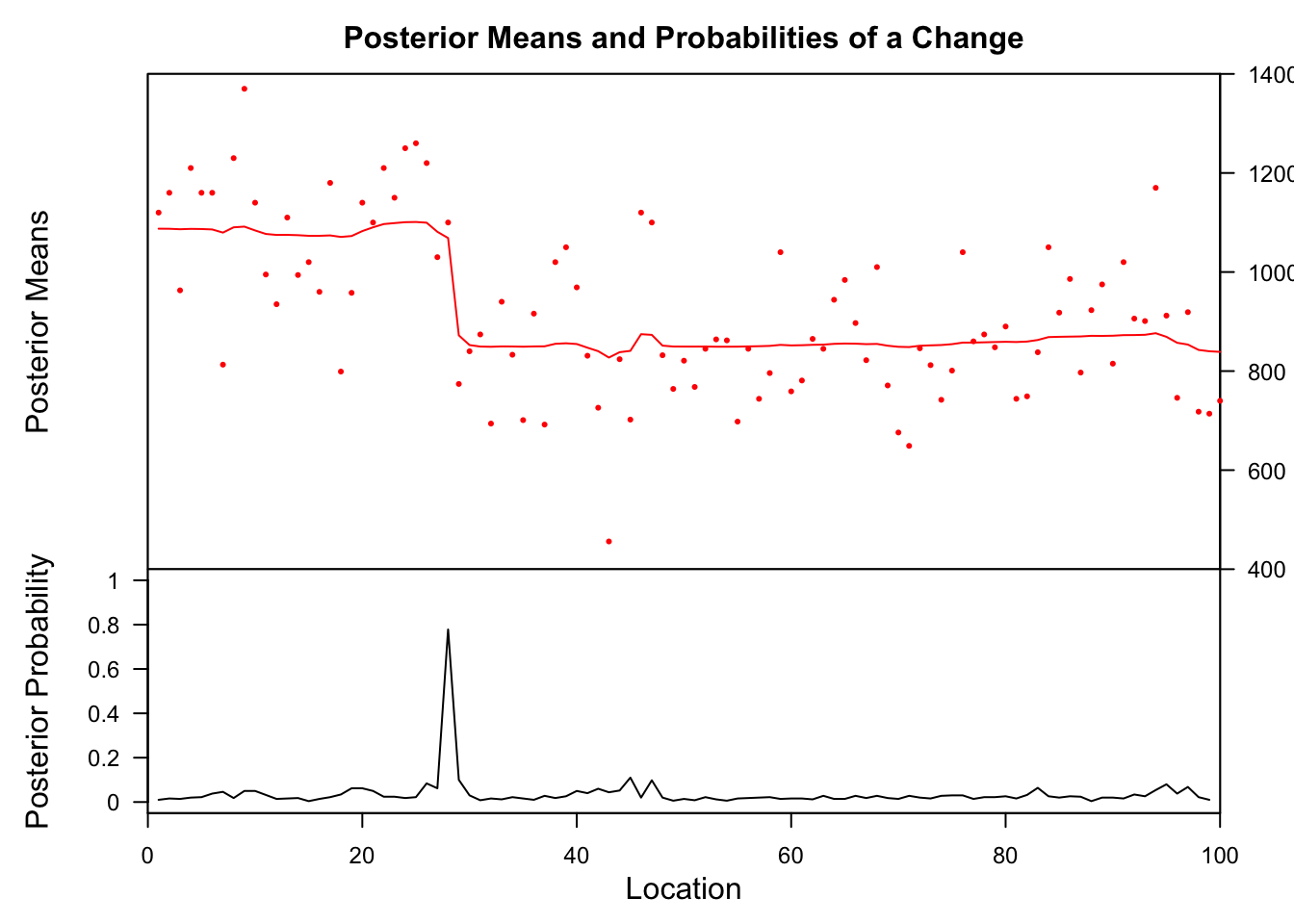
The lower posterior probability plot shows that at 1 location (looks like #28) the probability of a change is very loftier. Nosotros can get the verbal locations where probabilities are high (e.chiliad. > 70%) with this code:
bcp_sum <- as.data.frame(summary(bcp_x)) # Permit's filter the data frame and identify the yr: bcp_sum$id <- 1:length(ten) (sel <- bcp_sum[which(bcp_x$posterior.prob > 0.7), ]) # Get the yr: time(x)[sel$id] ## Probability X1 id ## 28 0.778 1068.629 28 ## [1] 1898 Likewise this method identified the correct yr of change.
strucchange
ocus_nile <- efp(Nile ~ 1, blazon = "OLS-CUSUM") op <- par(mfrow = c(1,2)) plot(ocus_nile) plot(ocus_nile, alpha = 0.01, alt.boundary = Truthful) 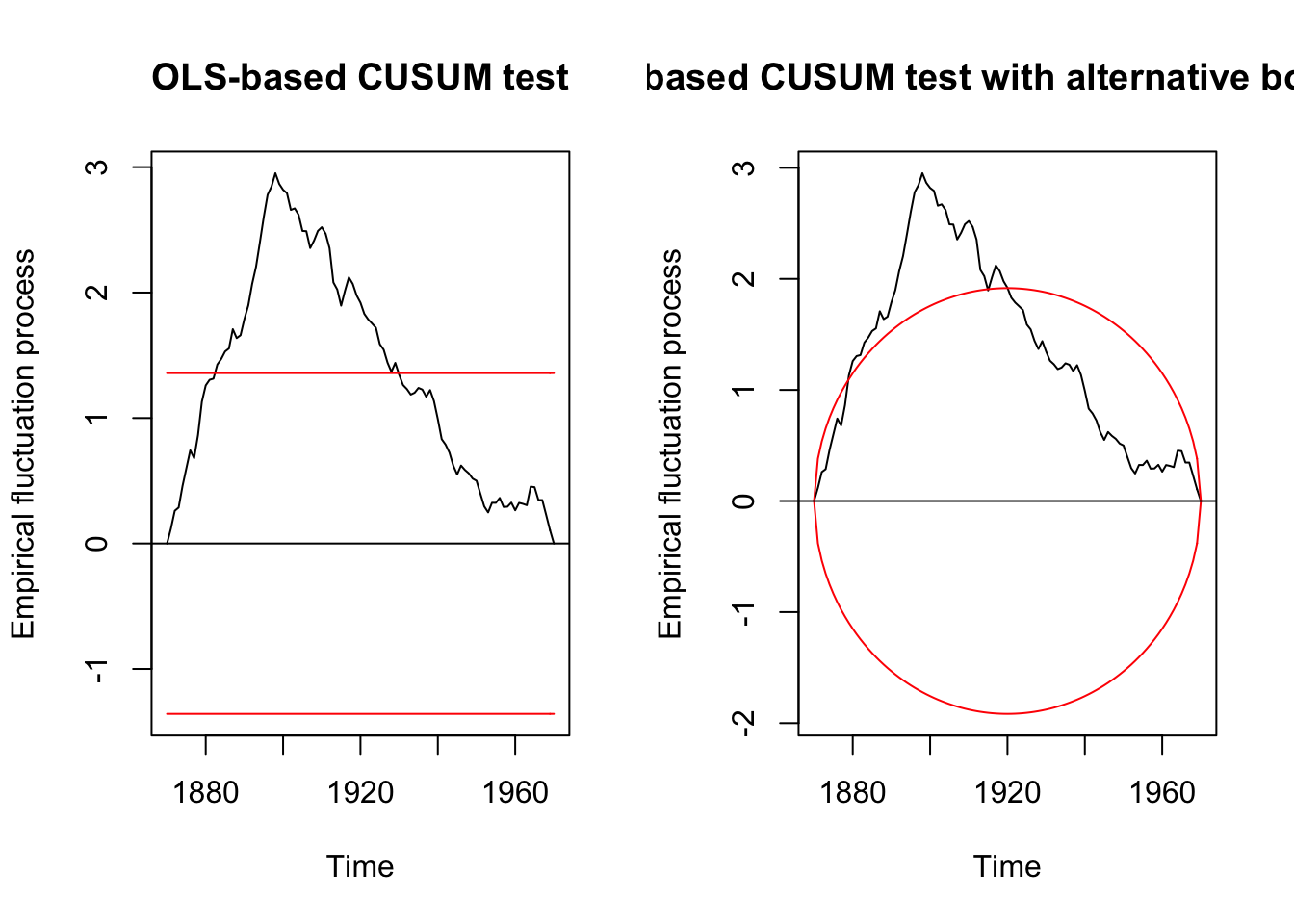
The efp function with the type "OLS-CUSUM" computes an empirical fluctuation procedure of OLS residuals which is plotted above. The process line shows a peak around 1900 which exceeds the boundaries and, hence, indicates a clear structural shift at that time.
To calculate the corresponding CUSUM and F exam statistics for structural alter (the first computed on the efp object):
sctest(ocus_nile) ## ## OLS-based CUSUM test ## ## data: ocus_nile ## S0 = 2.9518, p-value = 5.409e-08 fs_nile <- Fstats(Nile ~ 1) plot(fs_nile) 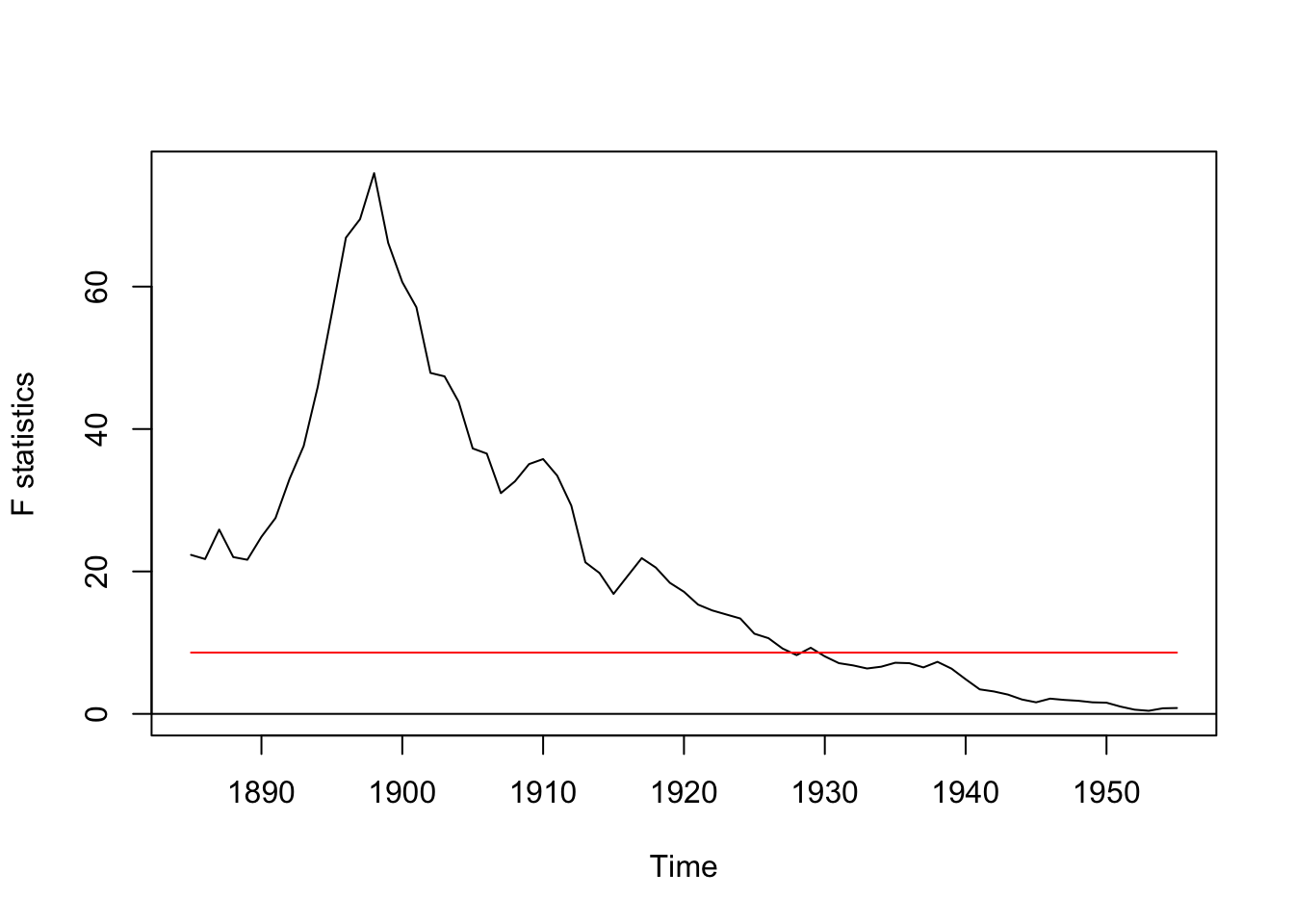
Both tests advise a significant alter in the time series.
Test for i breakpoint using the breakpoints() function → Annotation that the number of breakpoints have to be defined beforehand for this method!
bp_nile <- breakpoints(Nile ~ i) bp_nile ## ## Optimal 2-segment partition: ## ## Call: ## breakpoints.formula(formula = Nile ~ 1) ## ## Breakpoints at observation number: ## 28 ## ## Corresponding to breakdates: ## 1898 To check for multiple breaks, the breakpoint() function can be also applied to breakpoints objects with an explicit breaks argument (and so you really nest a breakpoints role in breakpoints():
breakpoints(bp_nile, breaks = 2) ## ## Optimal 3-segment partition: ## ## Telephone call: ## breakpoints.breakpointsfull(obj = bp_nile, breaks = 2) ## ## Breakpoints at ascertainment number: ## 28 83 ## ## Corresponding to breakdates: ## 1898 1953 # Nested syntax with three breaks: breakpoints(breakpoints(Nile ~ 1), breaks = 3) ## ## Optimal 4-segment partition: ## ## Telephone call: ## breakpoints.breakpointsfull(obj = breakpoints(Nile ~ ane), breaks = 3) ## ## Breakpoints at observation number: ## 28 68 83 ## ## Respective to breakdates: ## 1898 1938 1953 So how does one know how many breakpoints exist in the time series? Here, the comparison of BIC estimates for dissimilar numbers of breakpoint is useful:
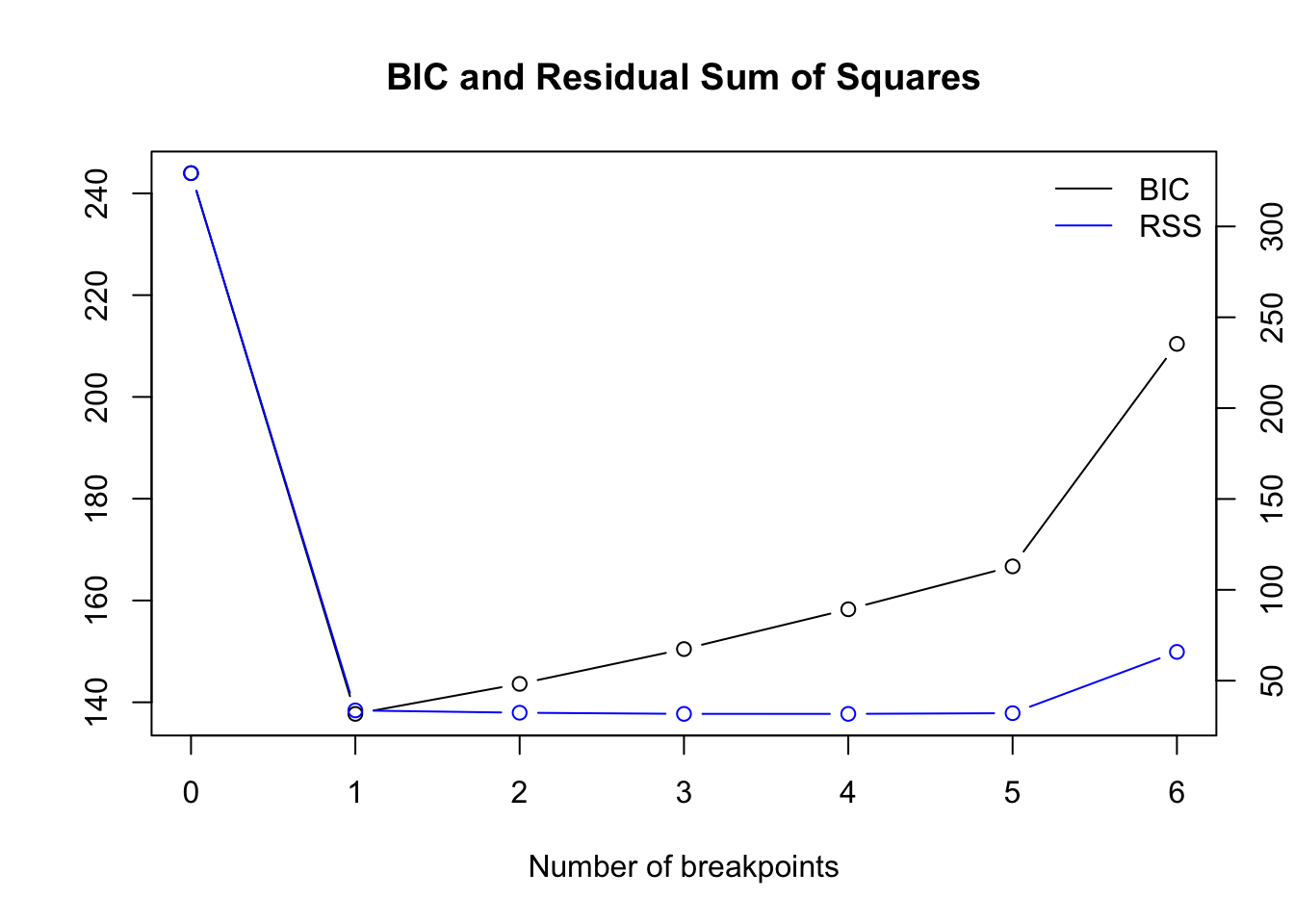
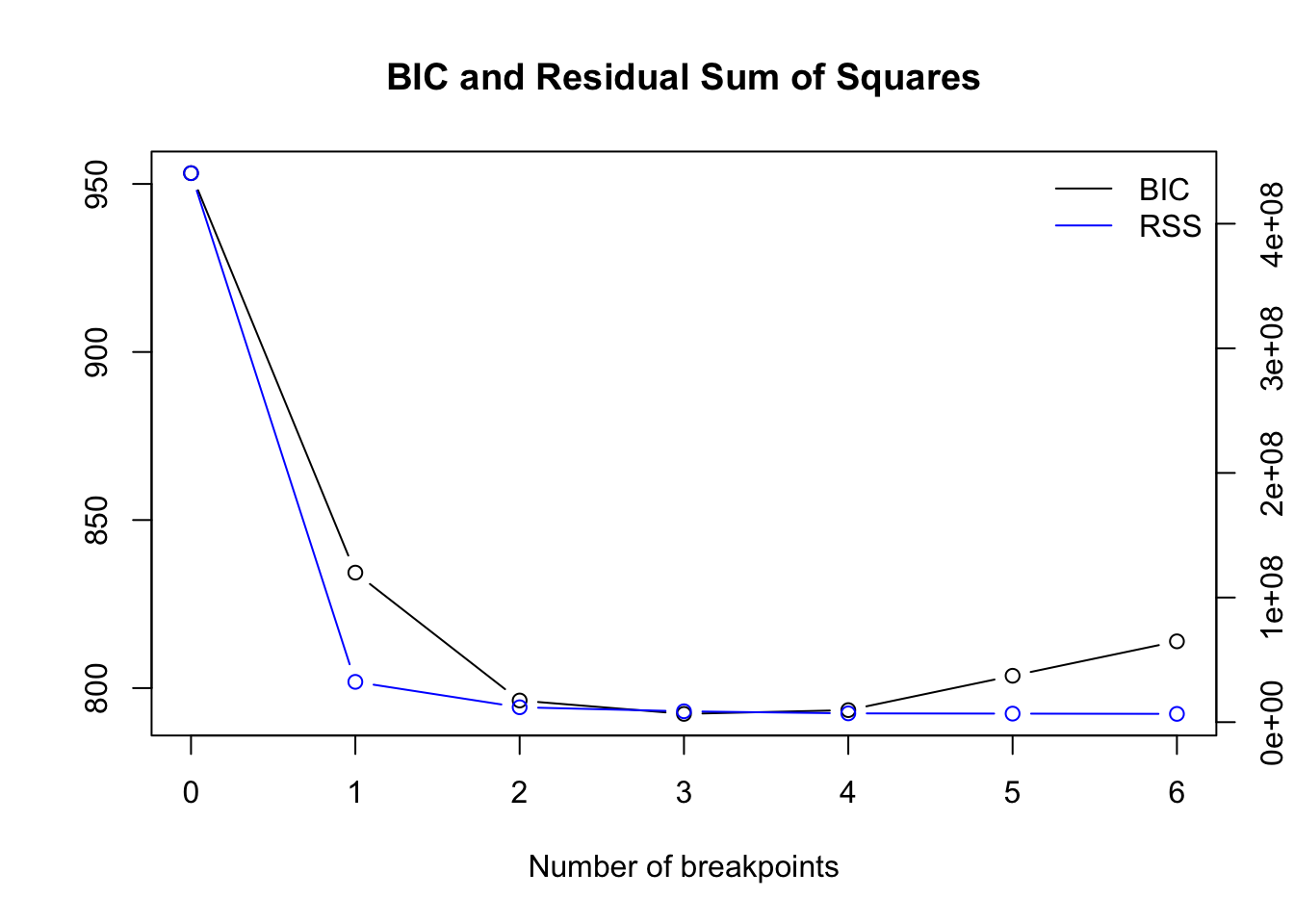
plot(bp_nile) 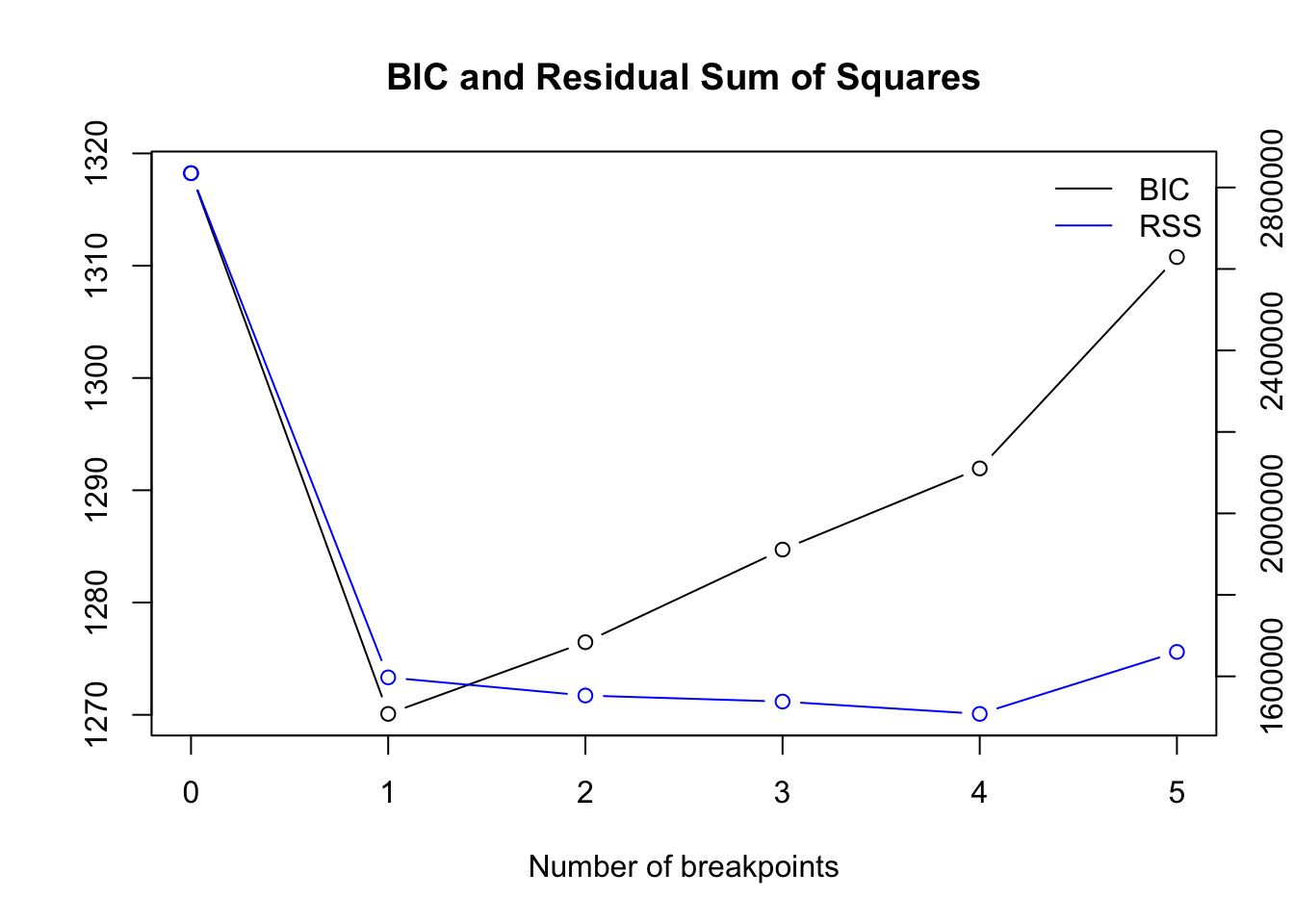
Based on the BIC we should choose one breakpoint.
To get the optimal number numerically instead of inspecting the plot each time, hither is a solution:
# get best model opt_bpts <- role(ten) { #x = bpts_sum$RSS["BIC",] due north <- length(x) everyman <- vector("logical", length = n-ane) everyman[1] <- False for (i in 2:due north) { lowest[i] <- x[i] < x[i-1] & ten[i] < ten[i+1] } out <- as.integer(names(ten)[lowest]) return(out) } bpts_sum <- summary(bp_nile) opt_brks <- opt_bpts(bpts_sum$RSS["BIC",]) opt_brks ## [i] 1 To go the location of the breakpoint(south):
## [one] 28 One can besides visualize the breakpoints in the time series plot with confidence intervals using the stats::confint() function:
ci_nile <- confint(bp_nile, breaks = opt_brks) plot(Nile) lines(ci_nile) 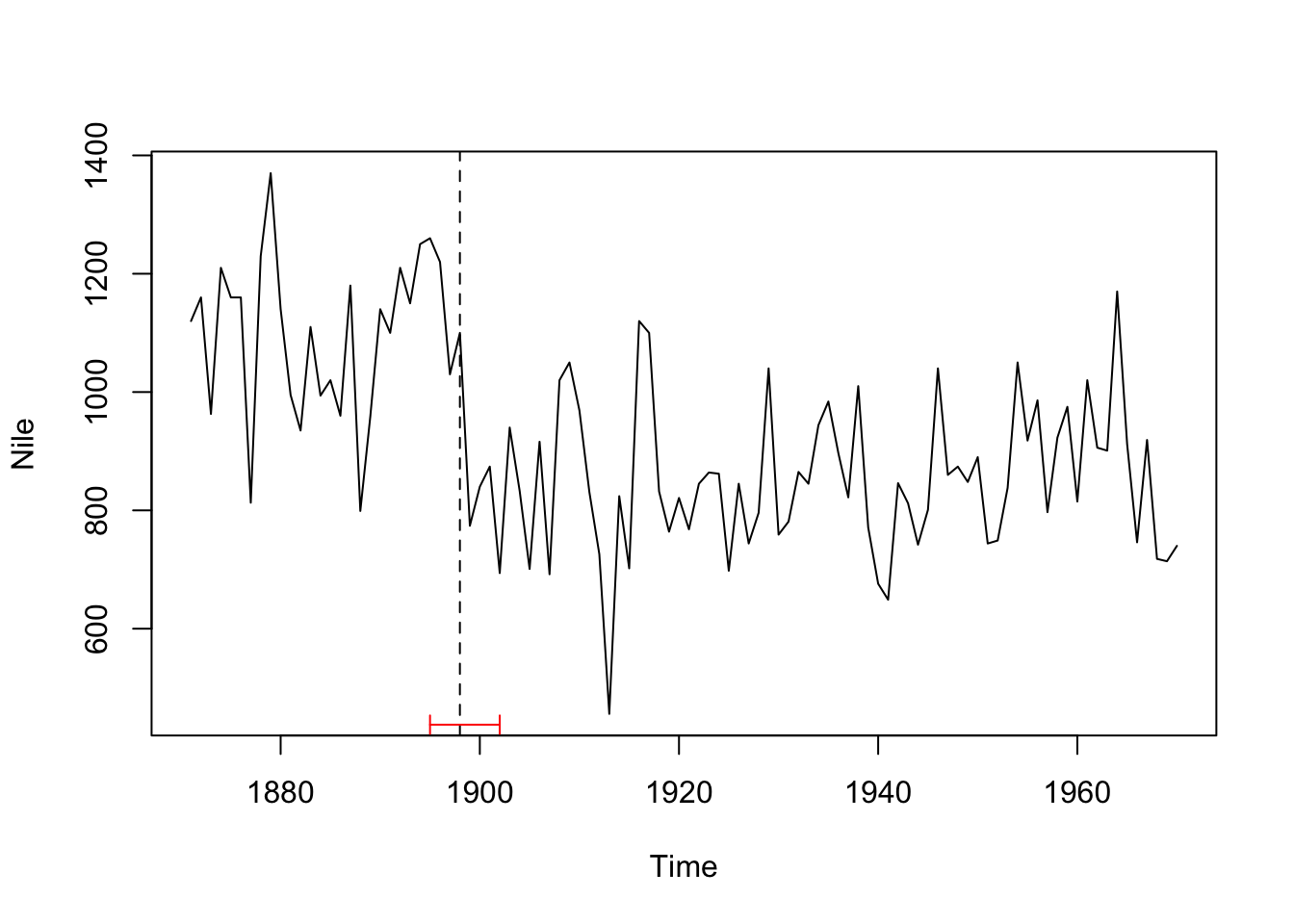
We can as well add the regression lines of the nothing model and our model with 1 breakpoint for comparison:
# zilch model fm0 <- lm(Nile ~ 1) coef(fm0) ## (Intercept) ## 919.35 # breakpoint model nile_fac <- breakfactor(bp_nile, breaks = one) fm1 <- lm(Nile ~ nile_fac - ane) coef(fm1) ## nile_facsegment1 nile_facsegment2 ## 1097.7500 849.9722 plot(Nile) lines(ci_nile) lines(ts(fitted(fm0), start = 1871), col = 3) lines(ts(fitted(fm1), offset = 1871), col = 4) lines(bp_nile) 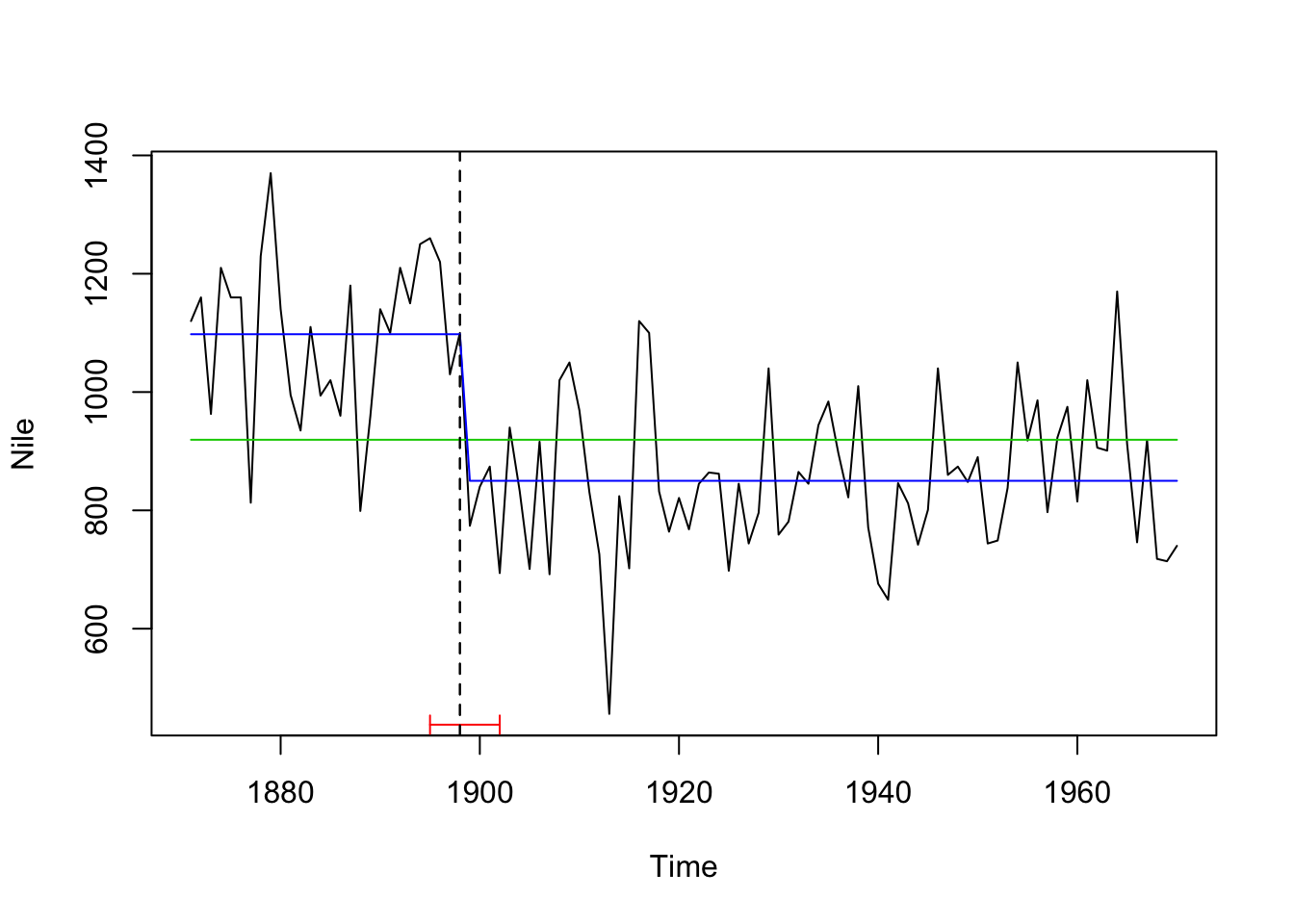
segmented
With this method, the number of breakpoints have to exist likewise specified beforehand similar to the strucchange::breakpoints() function:
Nile_df <- data.frame(Nile = every bit.numeric(Nile), Year = 1871:1970) seg_nile <- segmented(lm(Nile ~ 1, information = Nile_df), ~ Yr, psi = listing(Year = c(1900))) # using 1900 equally starting value summary(seg_nile) ## ## ***Regression Model with Segmented Human relationship(due south)*** ## ## Call: ## segmented.lm(obj = lm(Nile ~ one, data = Nile_df), seg.Z = ~Year, ## psi = listing(Twelvemonth = c(1900))) ## ## Estimated Suspension-Signal(s): ## Est. St.Err ## psi1.Year 1872.98 41.048 ## ## Meaningful coefficients of the linear terms: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 1147.4404 108.6654 10.559 <2e-16 *** ## U1.Year -2.7143 0.5404 -five.023 NA ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.ane ' ' 1 ## ## Residual standard fault: 151.3 on 97 degrees of freedom ## Multiple R-Squared: 0.2165, Adjusted R-squared: 0.2004 ## ## Convergence attained in 2 iter. (rel. alter 2.0964e-xvi) summary(seg_nile)$psi ## Initial Est. St.Err ## psi1.Year 1900 1872.98 41.04761 plot(Nile ~ Year, data = Nile_df, type = "l") plot(seg_nile, add=T) lines(seg_nile,col='reddish') 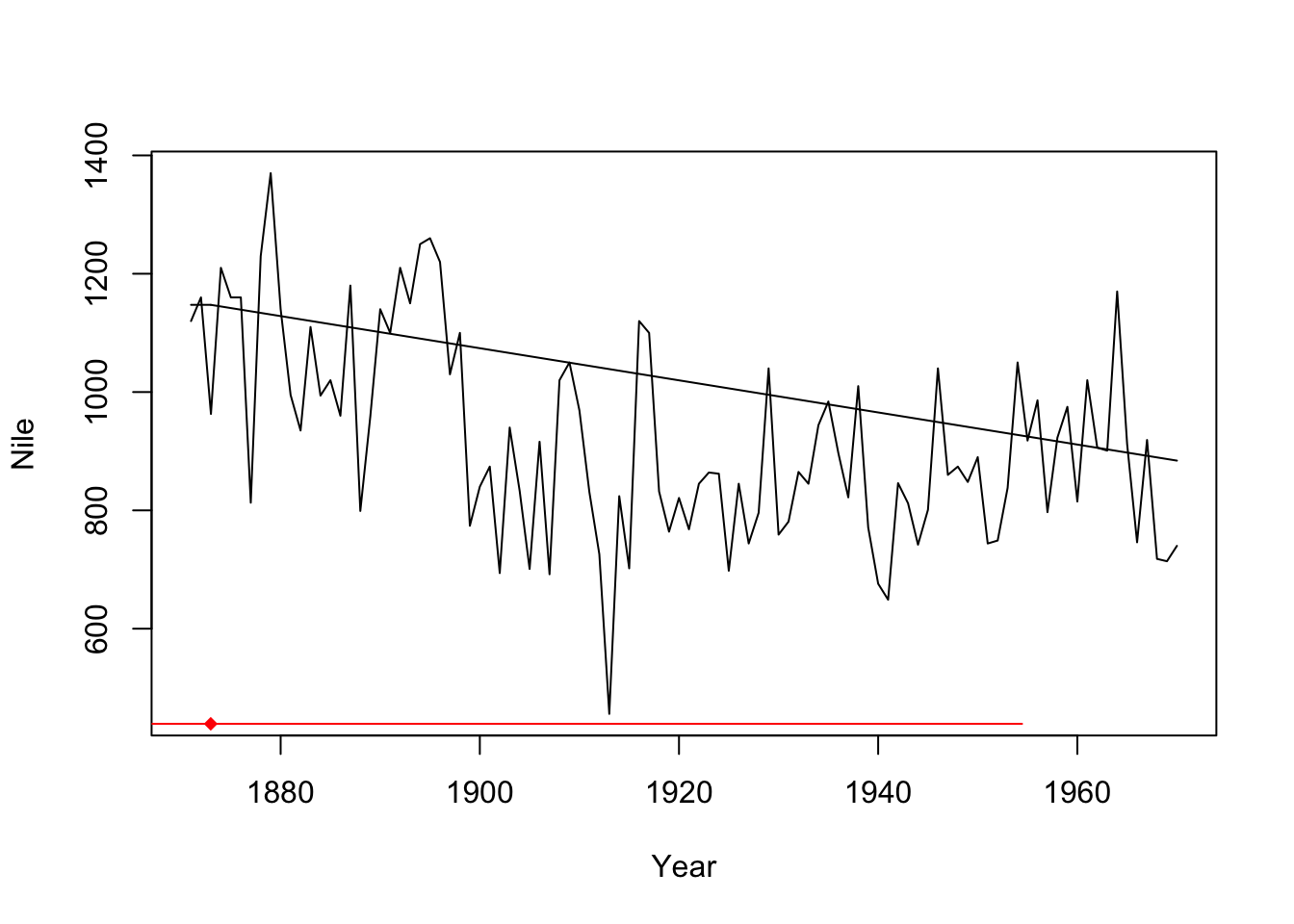
The segmented() function detects one change, but right at the start (1873). It seems to exist not devised for this kind of footstep modify.
tree
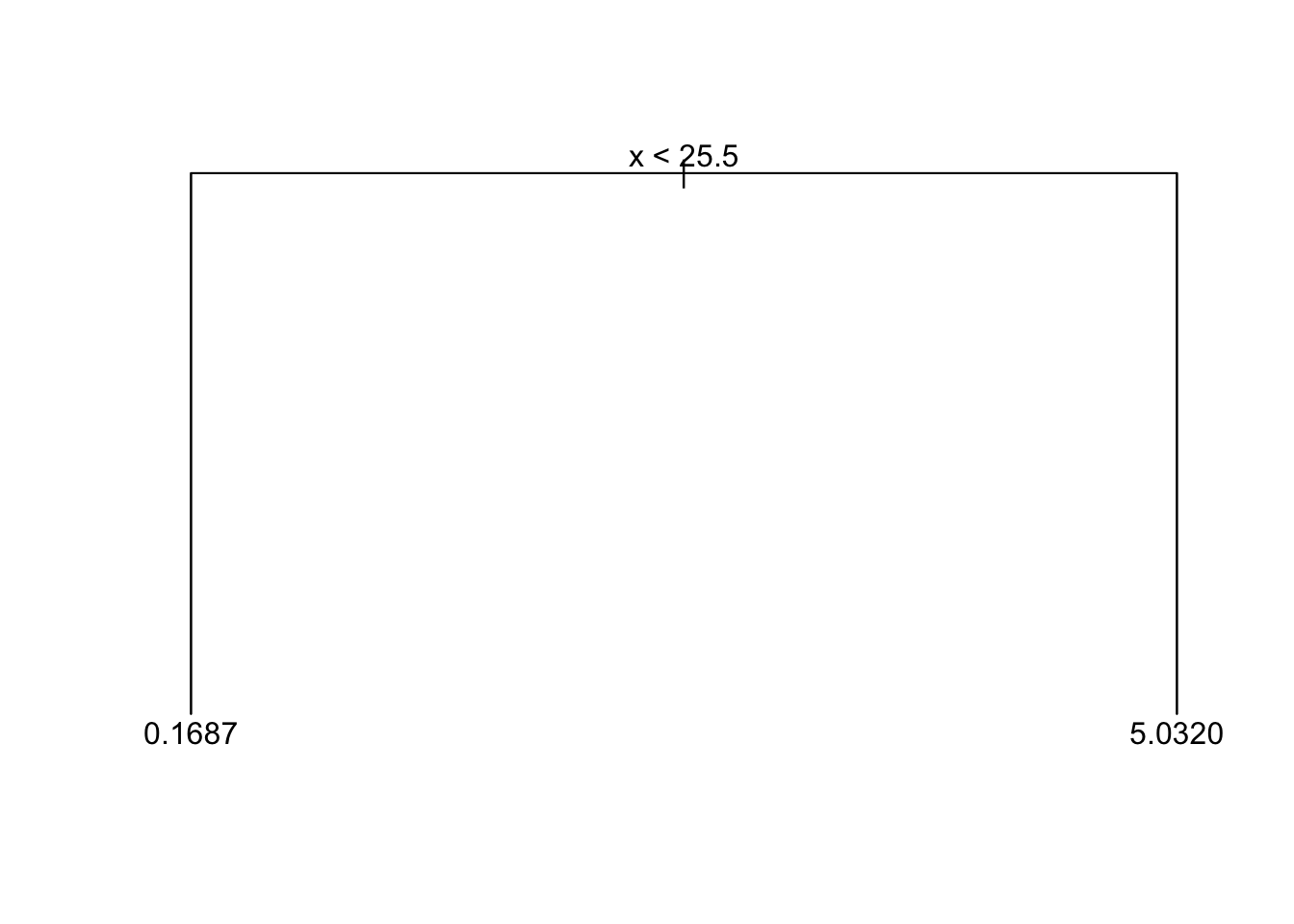
Nile_df <- data.frame(Nile = as.numeric(Nile), Year = 1871:1970) tree_nile <- tree(Nile ~ Year, data = Nile_df) summary(tree_nile) ## ## Regression tree: ## tree(formula = Nile ~ Year, data = Nile_df) ## Number of last nodes: six ## Residual hateful deviance: 13750 = 1293000 / 94 ## Distribution of residuals: ## Min. 1st Qu. Median Hateful third Qu. Max. ## -380.100 -62.160 -3.645 0.000 54.840 283.900 plot(tree_nile) text(tree_nile, pretty = 0) 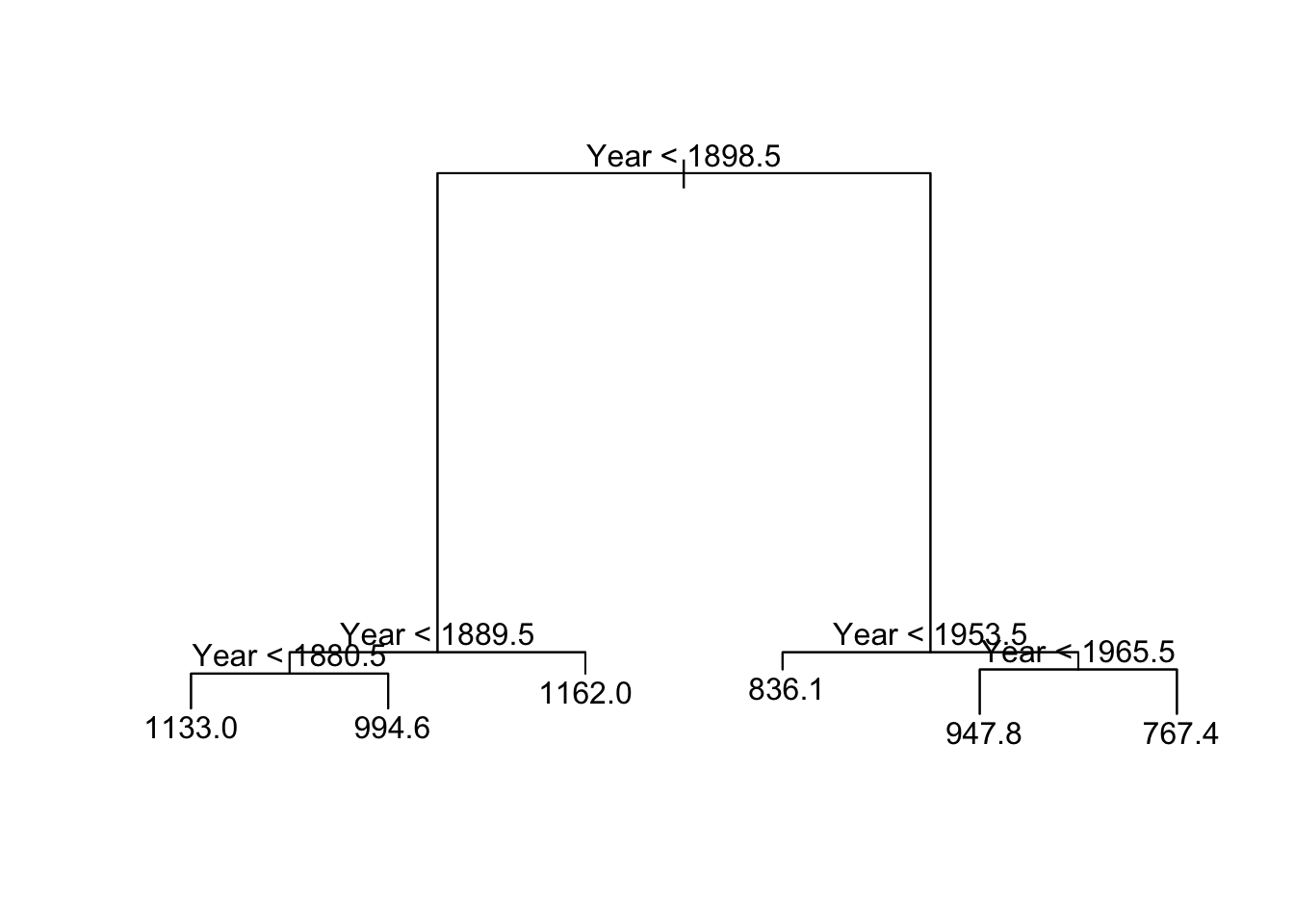
Also the tree() function finds correctly the change bespeak in the Nile time series.
Then allow's effort another time series…
Artificial data
fix.seed(one) # Normal distributed data with a single alter in mean (at x = 25/26) df <- information.frame( ten = 1:l, z = c(rnorm(25,0,1), rnorm(25,5,one)) ) plot(df$x, df$z, type = '50', xlab = '', ylab = '') lines(ten = ane:25, y = rep(0,25), col = 'cherry', lwd = 3) lines(10=26:50, y = rep(v,25), col = 'red', lwd = three) 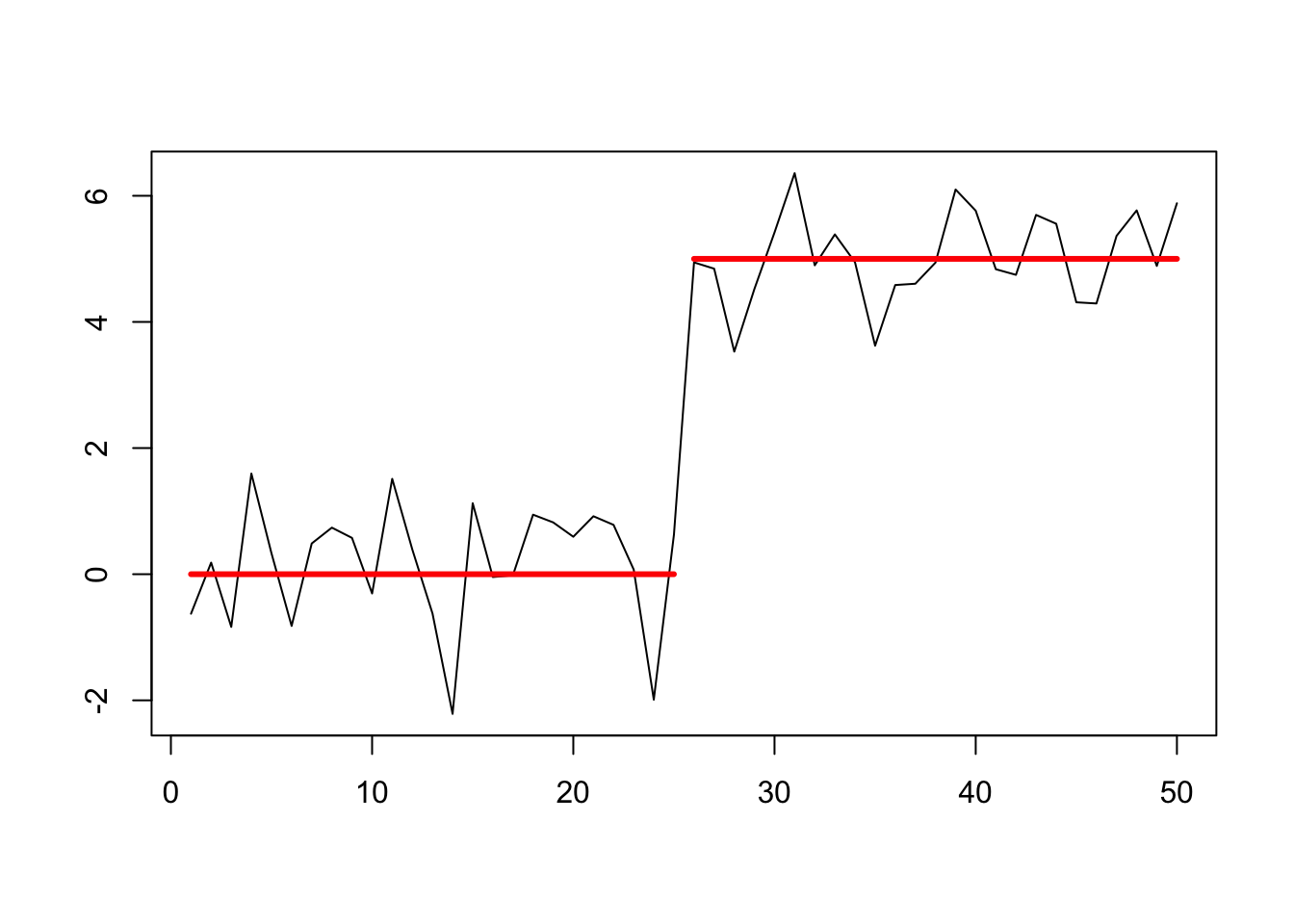
Since it is difficult to place the location of change points if data input objects for efp() and Fstats() are not a time series, I will convert df$z and apply z_ts similar to the Nile data (this will help identifying the row in the data of the changepoint location):
z_ts <- as.ts(df$z) changepoint
Testing for 1 modify point
## Created Using changepoint version 2.ii.two ## Changepoint type : Change in mean ## Method of analysis : AMOC ## Test Statistic : Normal ## Type of penalty : MBIC with value, eleven.73607 ## Minimum Segment Length : one ## Maximum no. of cpts : 1 ## Changepoint Locations : 25 Testing for several using PELT method and AIC penalty:
## Form 'cpt' : Changepoint Object ## ~~ : S4 class containing 12 slots with names ## cpttype engagement version information.fix method test.stat pen.type pen.value minseglen cpts ncpts.max param.est ## ## Created on : Fri April 26 15:58:35 2019 ## ## summary(.) : ## ---------- ## Created Using changepoint version two.ii.2 ## Changepoint type : Change in mean ## Method of analysis : PELT ## Test Statistic : Normal ## Type of penalty : AIC with value, iv ## Minimum Segment Length : 1 ## Maximum no. of cpts : Inf ## Changepoint Locations : 25 Also just 1 change indicate detected at x = 25.
Testing for several using PELT method and CROPS penalisation:
## [1] "Maximum number of runs of algorithm = 13" ## [1] "Completed runs = two" ## [1] "Completed runs = 3" ## [1] "Completed runs = 5" ## [1] "Completed runs = 9" ## [i] "Completed runs = 11" ## [1] "Completed runs = 12" ## Created Using changepoint version 2.two.2 ## Changepoint type : Change in mean ## Method of analysis : PELT ## Examination Statistic : Normal ## Type of punishment : CROPS with value, 1 25 ## Minimum Segment Length : ane ## Maximum no. of cpts : Inf ## Changepoint Locations : ## Number of segmentations recorded: seven with between i and 12 changepoints. ## Punishment value ranges from: 1 to 3.023723 ## [,1] [,2] [,three] [,4] [,5] [,vi] [,7] [,viii] [,9] [,ten] [,11] [,12] ## [1,] 3 four 13 14 23 24 25 29 34 37 44 46 ## [2,] 3 4 thirteen fourteen 23 24 25 29 34 37 NA NA ## [three,] 3 4 xiii fourteen 23 24 25 29 NA NA NA NA ## [4,] 3 iv 13 xiv 23 24 25 NA NA NA NA NA ## [five,] 13 xiv 23 24 25 NA NA NA NA NA NA NA ## [six,] 13 xiv 25 NA NA NA NA NA NA NA NA NA ## [seven,] 25 NA NA NA NA NA NA NA NA NA NA NA CROPS does not give an optimal set of changepoints, thus, we may wish to explore farther by looking at the diagnostic plot and the associated penalty transition points:
plot(cpt2, diagnostic = True) 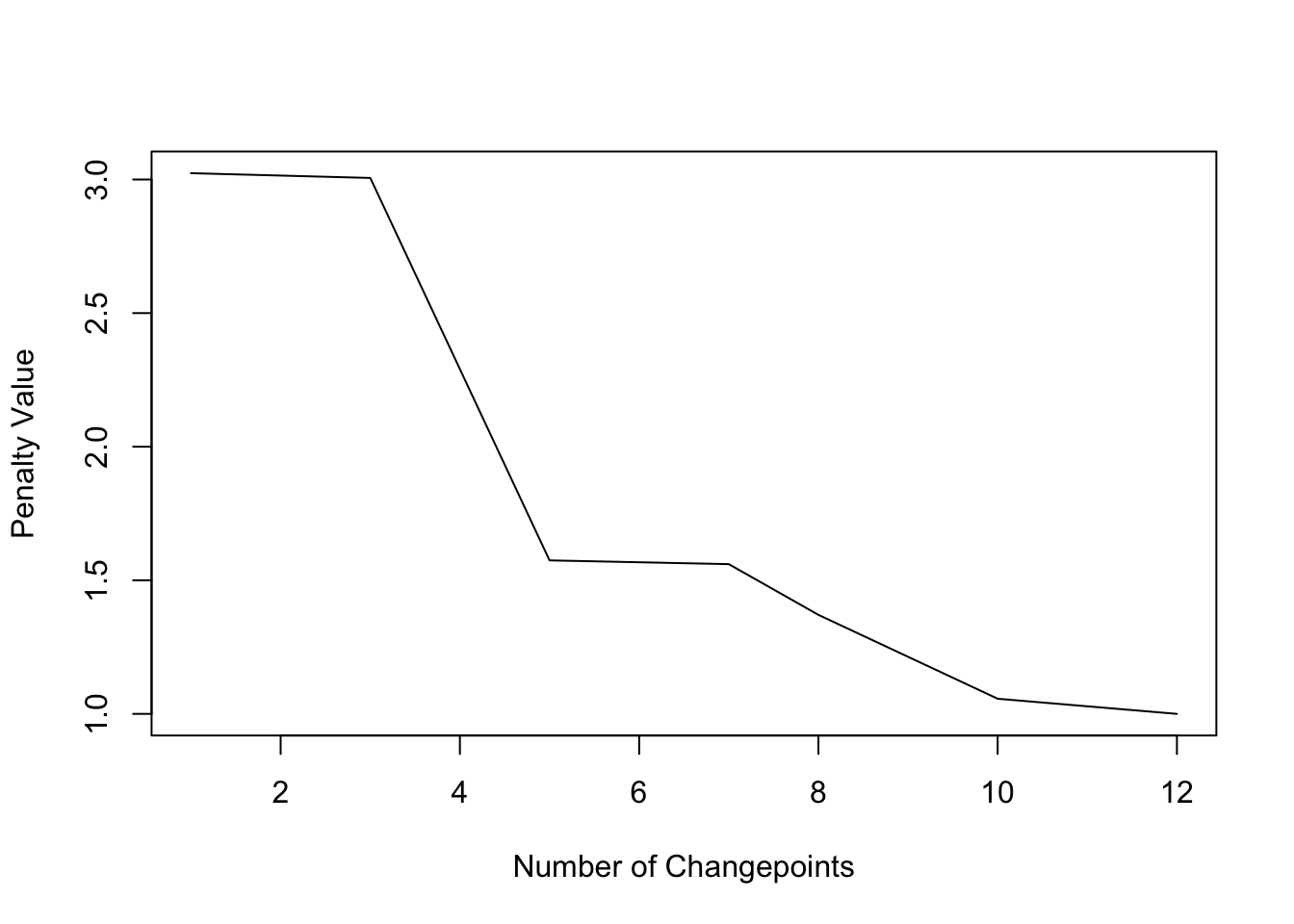
With the PELT method and CROPS penalty 5 change points are detected. So the choice of penalization can be highly relevant.
bcp
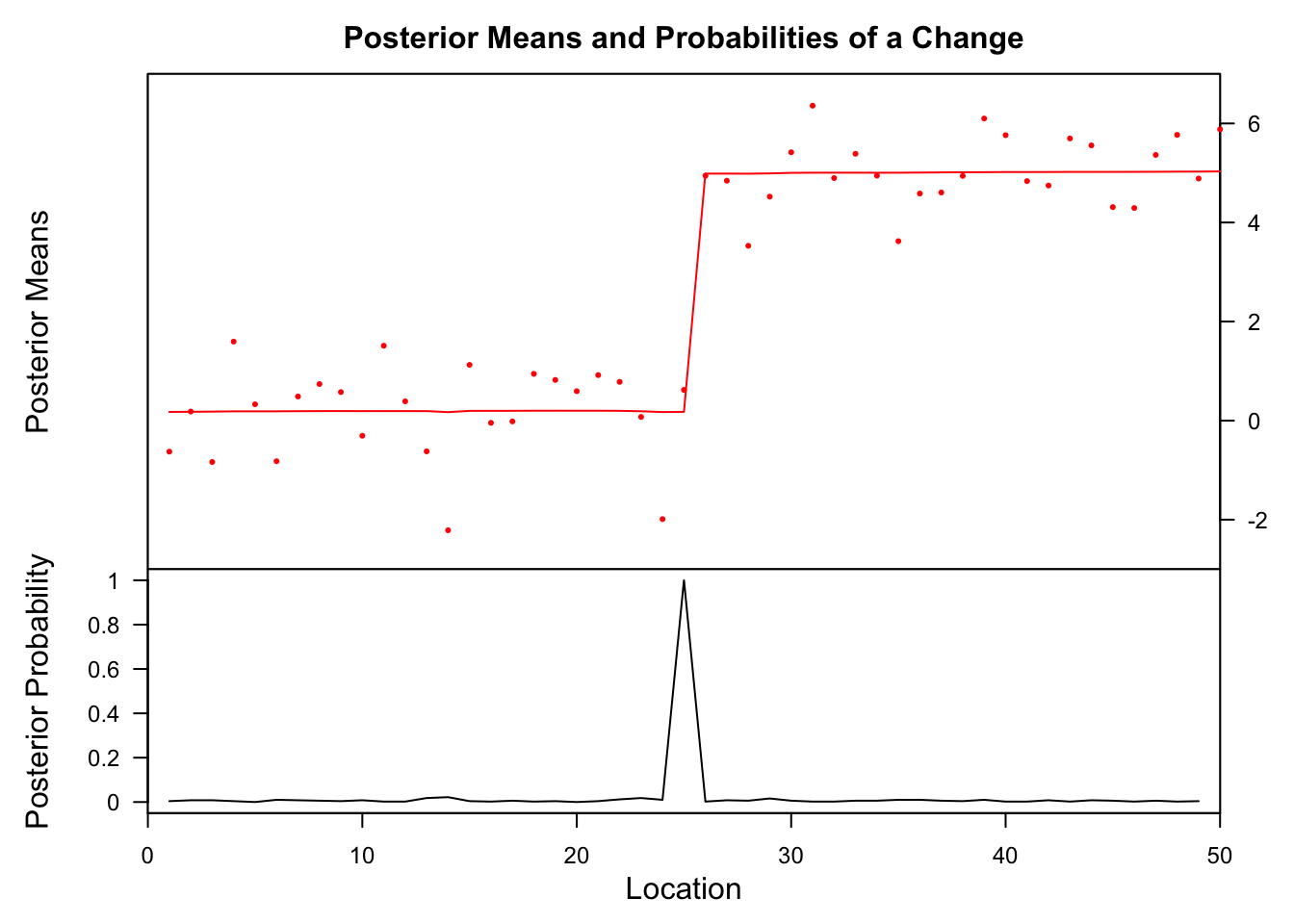
## Probability X1 id ## 25 1 0.176899 25 strucchange
Generalized fluctuation test 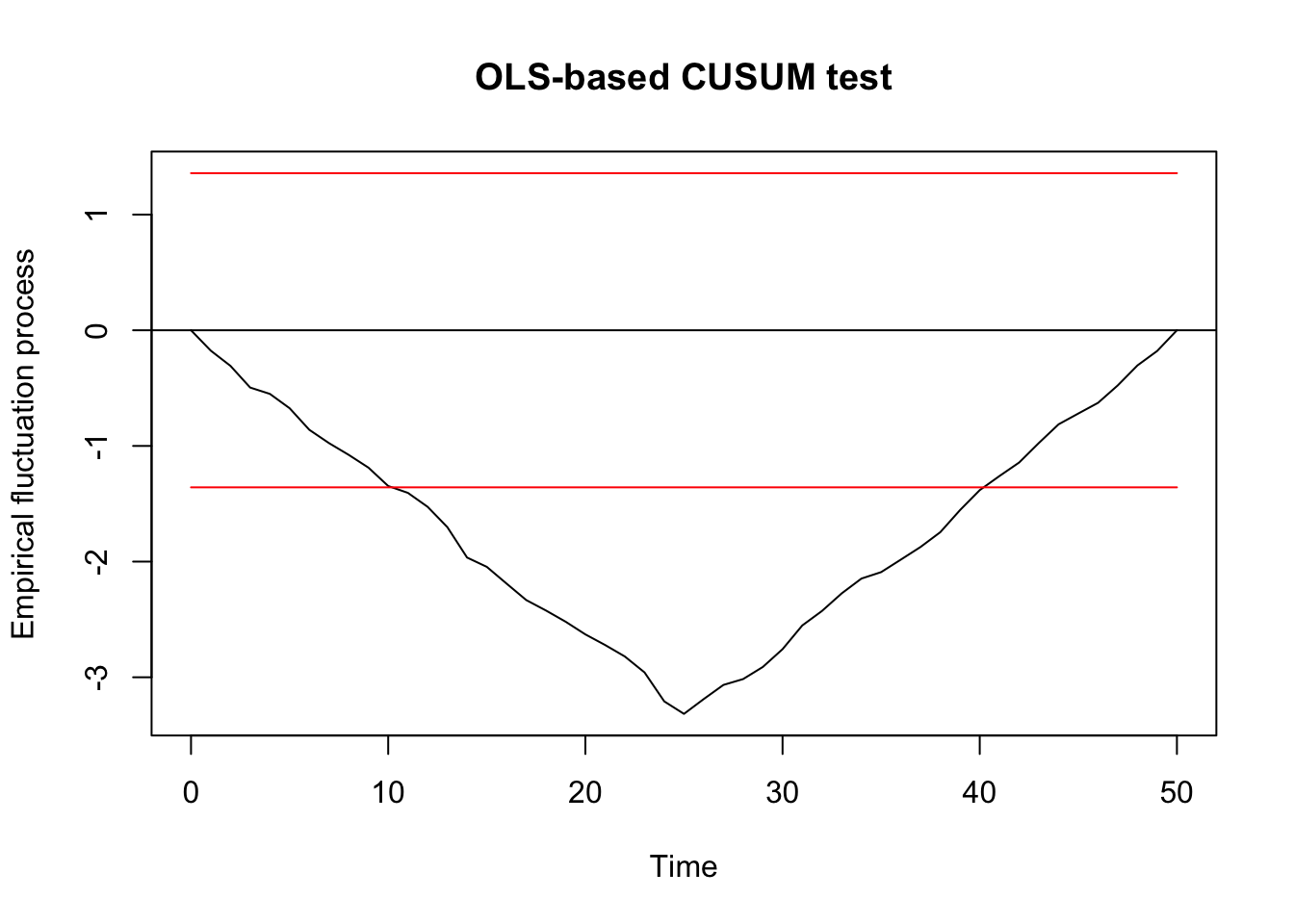
## ## OLS-based CUSUM test ## ## data: ocus_mod ## S0 = 3.3164, p-value = 5.593e-10 F examination
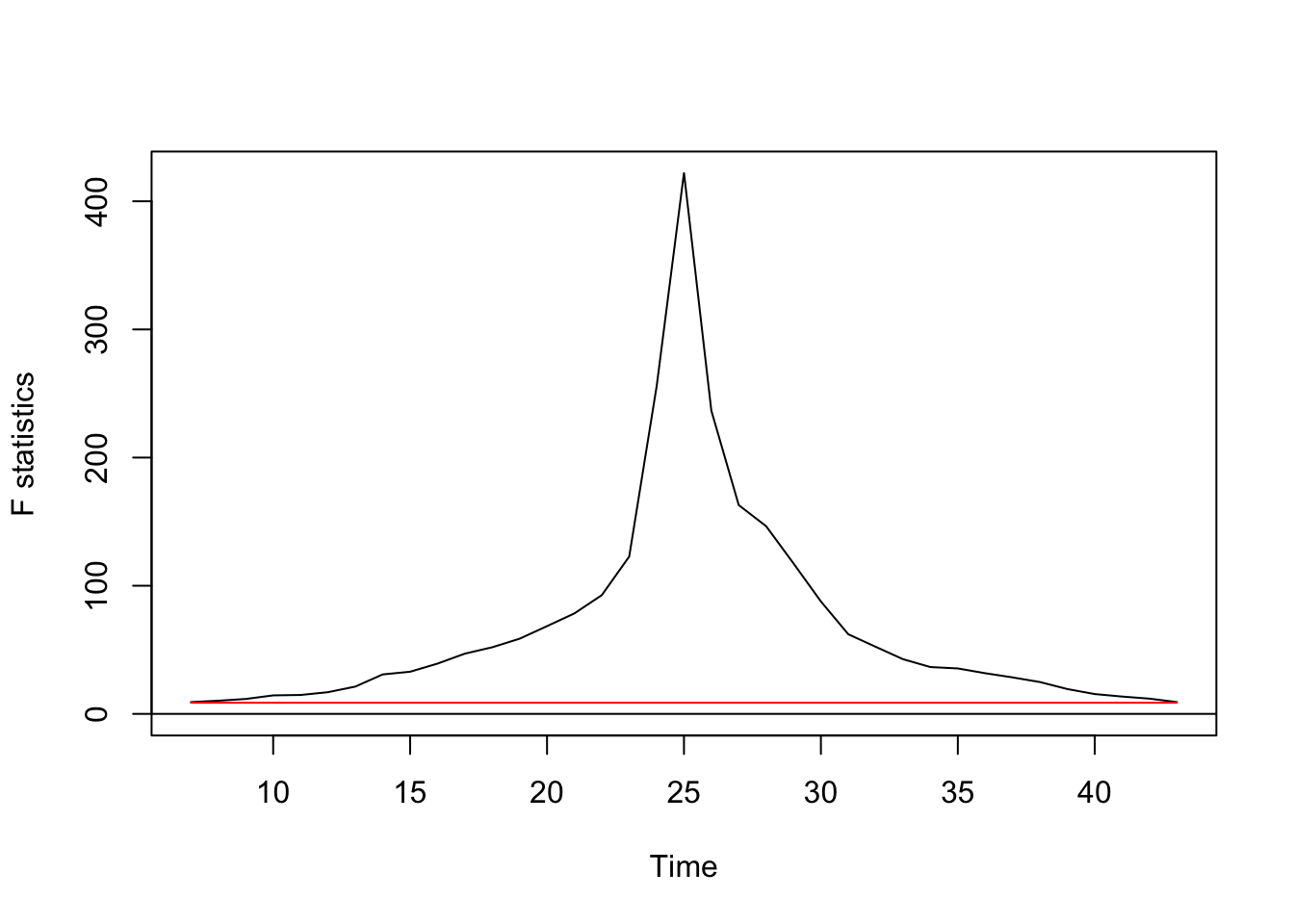
Regression break points
Optimal number of breakpoints:
## [1] 1 Location of breakpoint:
## [1] 25 ci_mod <- confint(bpts, breaks = opt_brks) plot(z ~ ten, information = df, blazon = "fifty") for (i in ane: opt_brks) { abline(v = df$ten[ci_mod$confint[i,2]], col = "bluish") abline(five = df$x[ci_mod$confint[i,1]], col = "red", lty = 3) abline(v = df$10[ci_mod$confint[i,3]], col = "ruby-red", lty = 3) } ## fit zilch hypothesis model and model with 1 breakpoint fm0 <- lm(z ~ 1, information = df) x_fac <- breakfactor(bpts2, breaks = 1) fm1 <- lm(z ~ x_fac - 1, information = df) fm1_coef <- coef(fm1) fit1 <- fitted(fm1)[i:best_brk] fit2 <- fitted(fm1)[(best_brk+one):max(df$x)] # add to previous plot lines(df$x, fitted(fm0), col = 3) lines(df$x[ane:best_brk], fit1, col = "orange") lines(df$10[(best_brk+1):max(df$ten)],fit2, col = "orange") 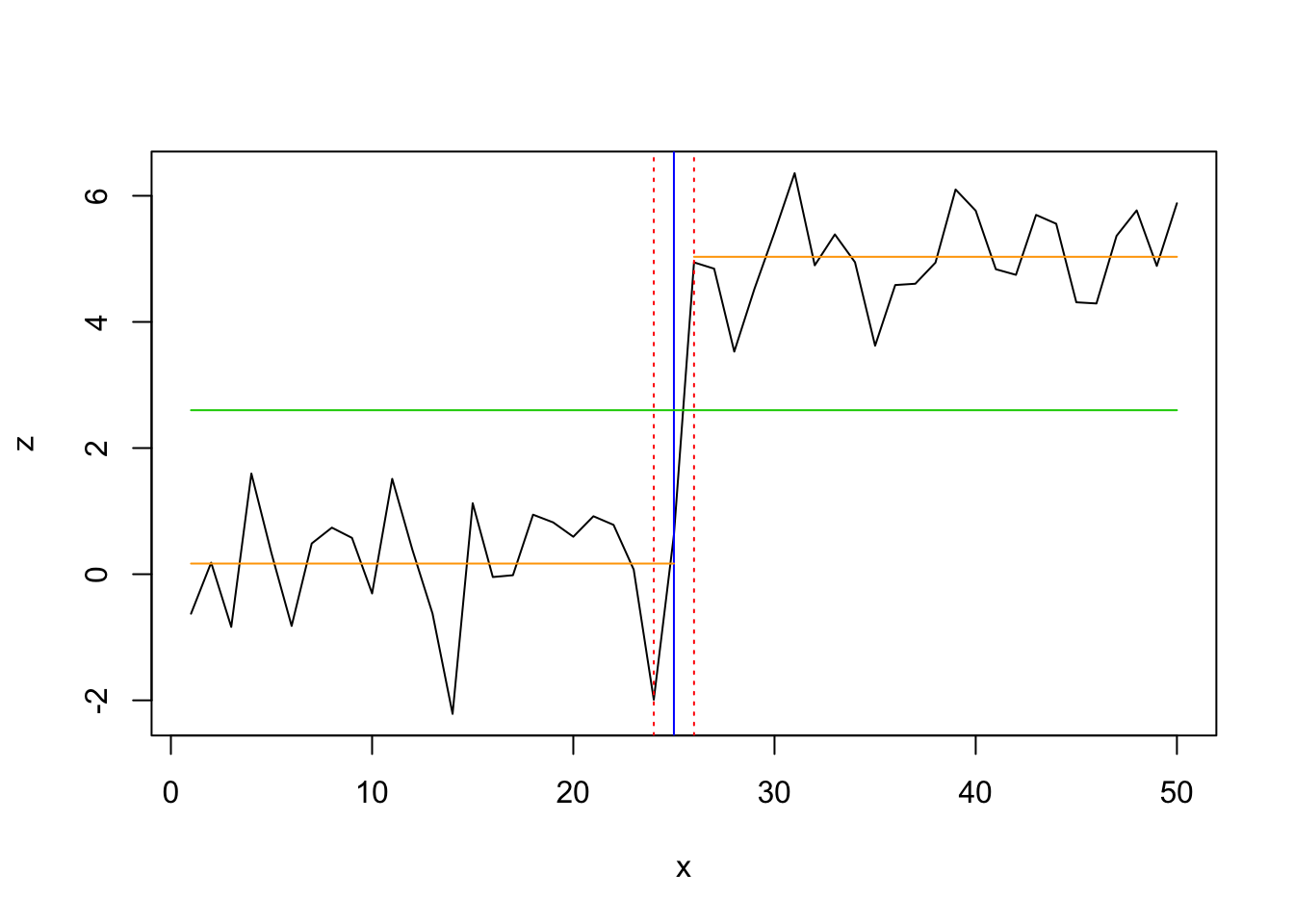
segmented
lin_mod <- lm(z ~ x, data = df) segm_mod <- segmented(lin_mod, seg.Z = ~x, psi=20) summary(segm_mod)$psi ## Initial Est. St.Err ## psi1.x 20 xiii.99996 5.525805 plot(z ~ 10, data = df, pch=16) plot(segm_mod, add=T) lines(segm_mod,col='red') 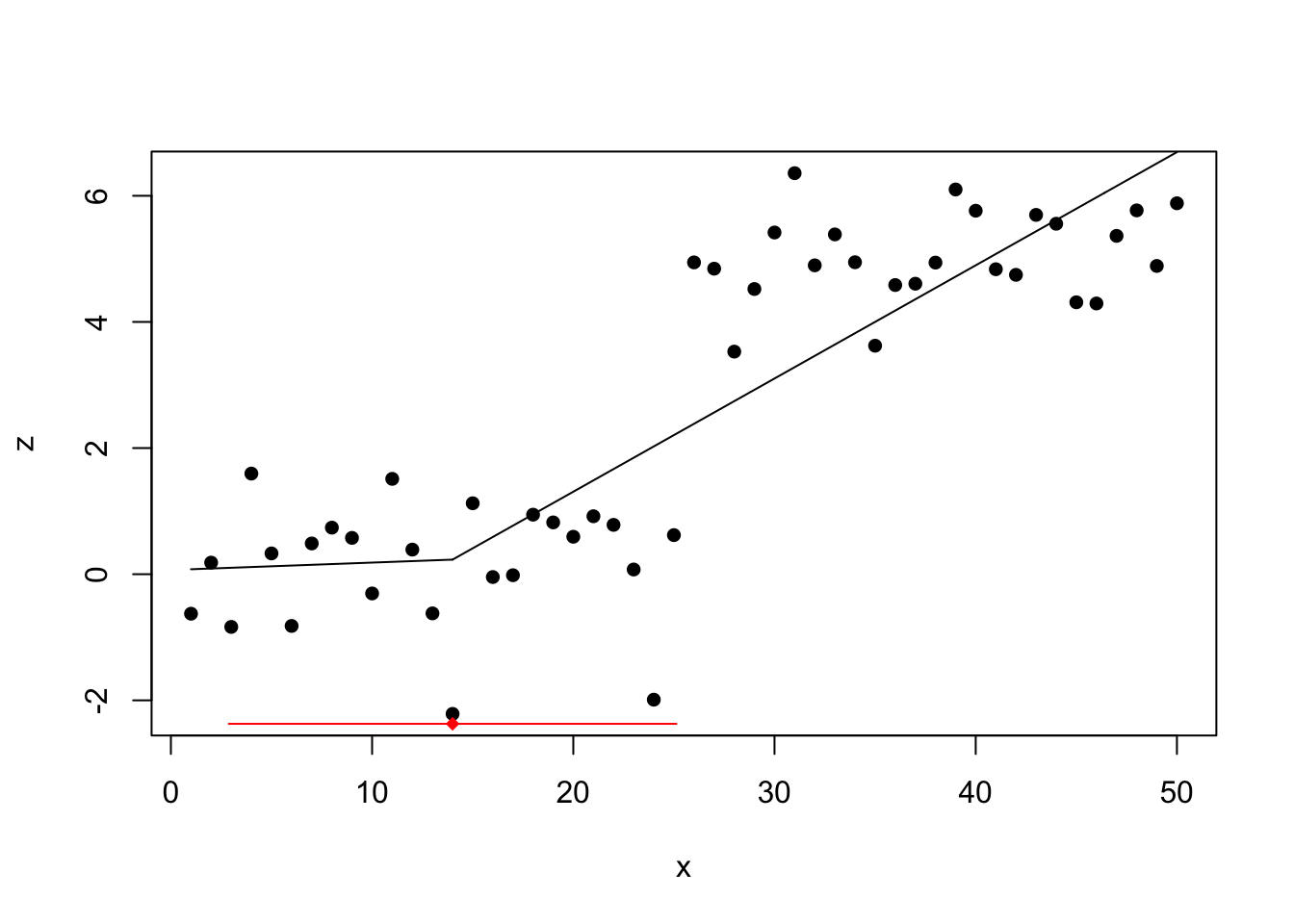
The detected change point lies around 14 with a wide confidence interval.
tree
three changes in hateful
set.seed(2) # Normal distributed information with 3 modify in hateful (at ten = 10/eleven, 25/26, 45/46) df <- data.frame( x = 1:l, z=c(rnorm(10, 1, sd = 0.5), rnorm(15, 0, sd = 0.5), rnorm(20, two, sd = 0.v), rnorm(5, 0.5 , sd = 0.5)) ) plot(df$x, df$z, type = 'l', xlab = '', ylab = '') lines(x = 1:x, y = rep(1,x), col = 'red', lwd = iii) lines(ten = 11:25, y = rep(0,15), col = 'carmine', lwd = three) lines(10 = 26:45, y = rep(ii,20), col = 'red', lwd = 3) lines(x = 46:fifty, y = rep(0.5,5), col = 'red', lwd = 3) 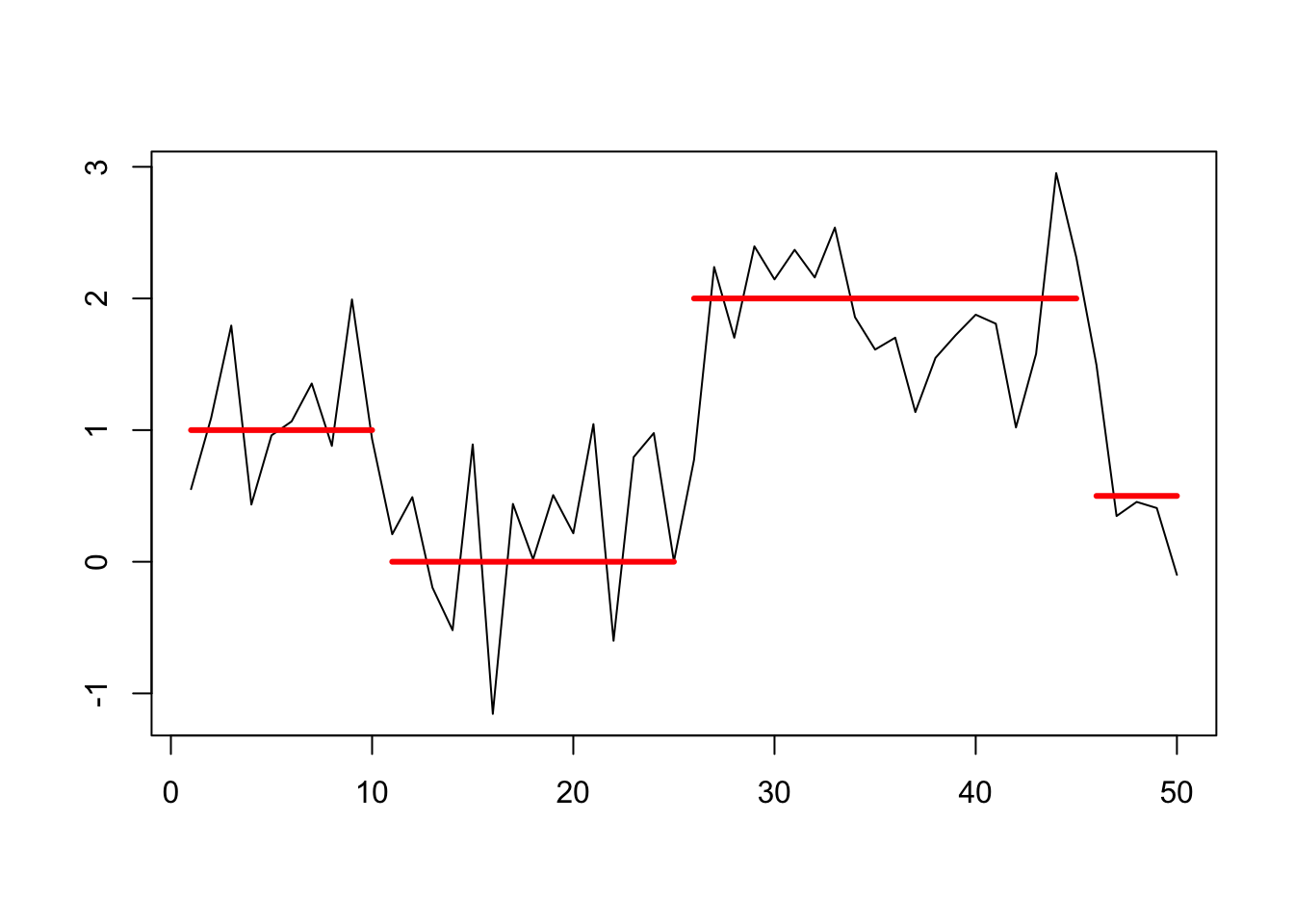
z_ts <- as.ts(df$z) changepoint
Testing for 1 change signal → naught detected
## Created Using changepoint version 2.2.2 ## Changepoint blazon : Change in mean ## Method of analysis : AMOC ## Test Statistic : Normal ## Type of punishment : MBIC with value, 11.73607 ## Minimum Segment Length : 1 ## Maximum no. of cpts : 1 ## Changepoint Locations : Testing for several using PELT method and AIC penalty → 3 modify points detected
## Class 'cpt' : Changepoint Object ## ~~ : S4 course containing 12 slots with names ## cpttype date version data.set method examination.stat pen.type pen.value minseglen cpts ncpts.max param.est ## ## Created on : Fri April 26 15:58:35 2019 ## ## summary(.) : ## ---------- ## Created Using changepoint version 2.2.two ## Changepoint blazon : Change in mean ## Method of analysis : PELT ## Test Statistic : Normal ## Type of punishment : AIC with value, 4 ## Minimum Segment Length : i ## Maximum no. of cpts : Inf ## Changepoint Locations : 10 26 46 Testing for several using PELT method and CROP type:
## [1] "Maximum number of runs of algorithm = 9" ## [1] "Completed runs = ii" ## [i] "Completed runs = 3" ## [1] "Completed runs = 5" ## [ane] "Completed runs = 8" ## Created Using changepoint version 2.two.two ## Changepoint type : Change in mean ## Method of analysis : PELT ## Examination Statistic : Normal ## Type of penalization : CROPS with value, 1 25 ## Minimum Segment Length : 1 ## Maximum no. of cpts : Inf ## Changepoint Locations : ## Number of segmentations recorded: vii with between 0 and 7 changepoints. ## Penalty value ranges from: 1 to 14.06746 In the following social club are change points detected:
cpts_ord(cpts.total(cpt2)) ## [1] 26 46 10 15 xvi 33 43 The diagnostic plot shows that the model with only 3 changepoints is the well-nigh parsimonious:
plot(cpt2, diagnostic = TRUE) 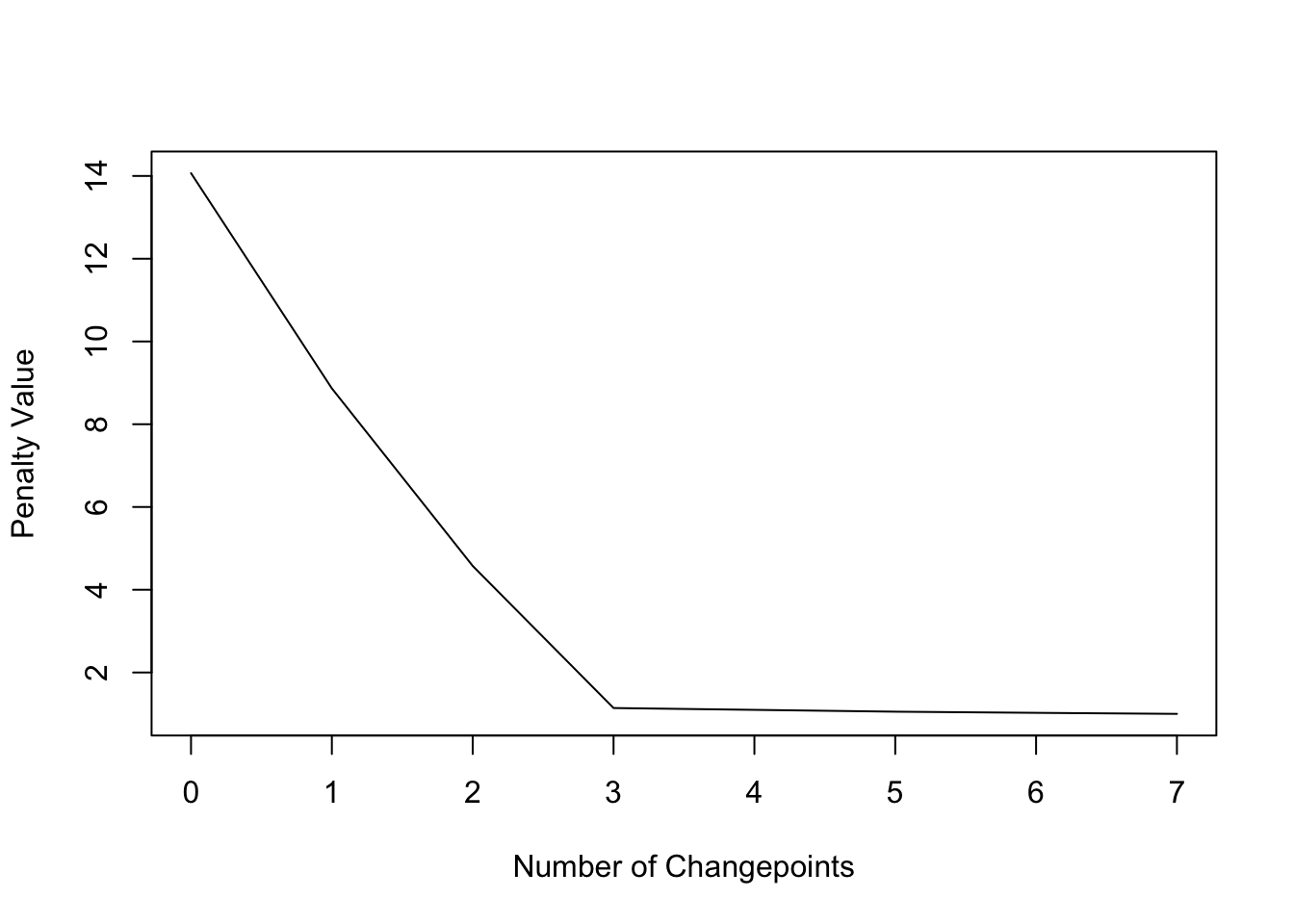
plot(cpt2, ncpts = 3) 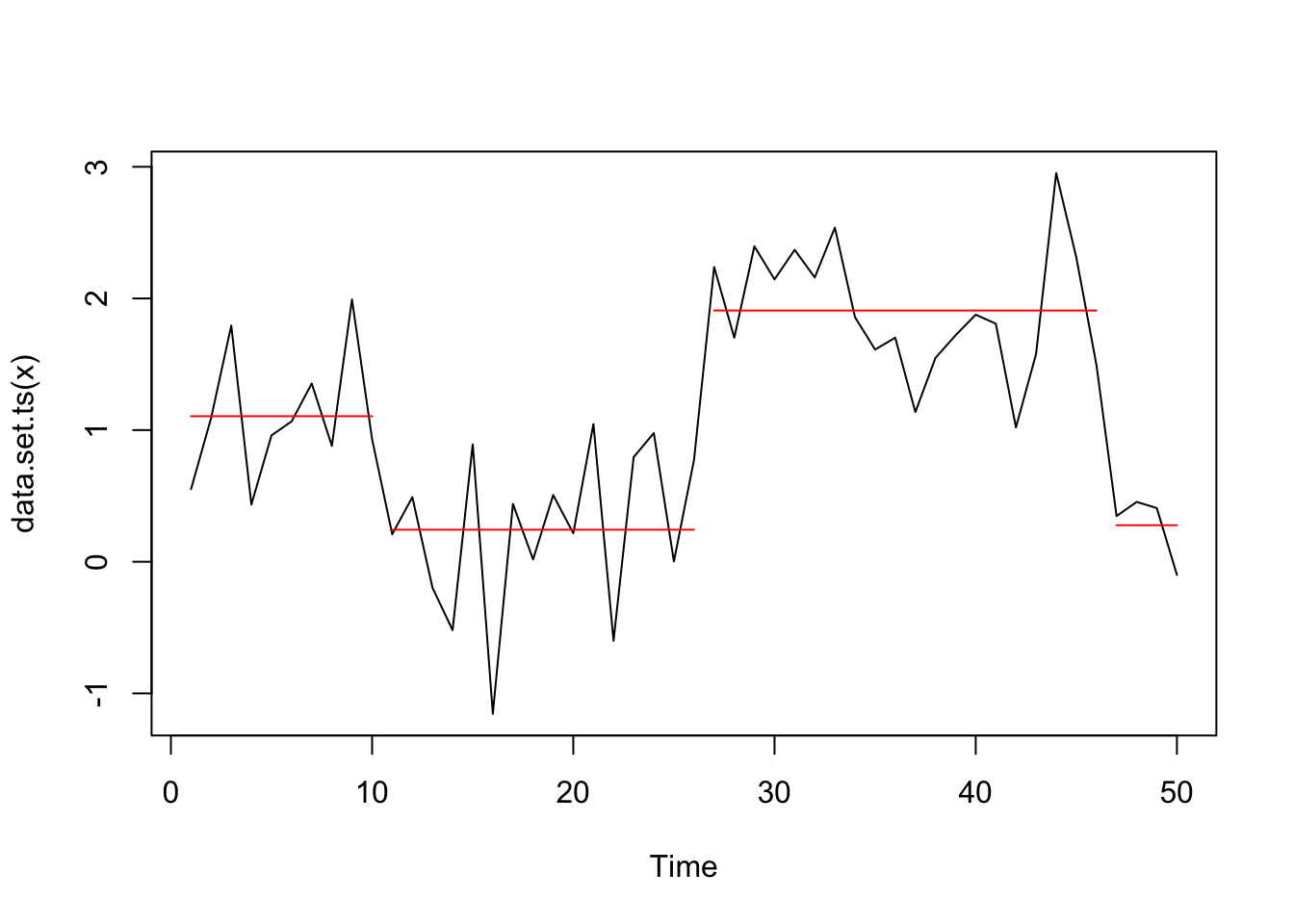
So also with the Crop penalty type we detect in this case the 3 changepoints only only when using the diagnostic plot to identify the appropriate number of changes.
bcp
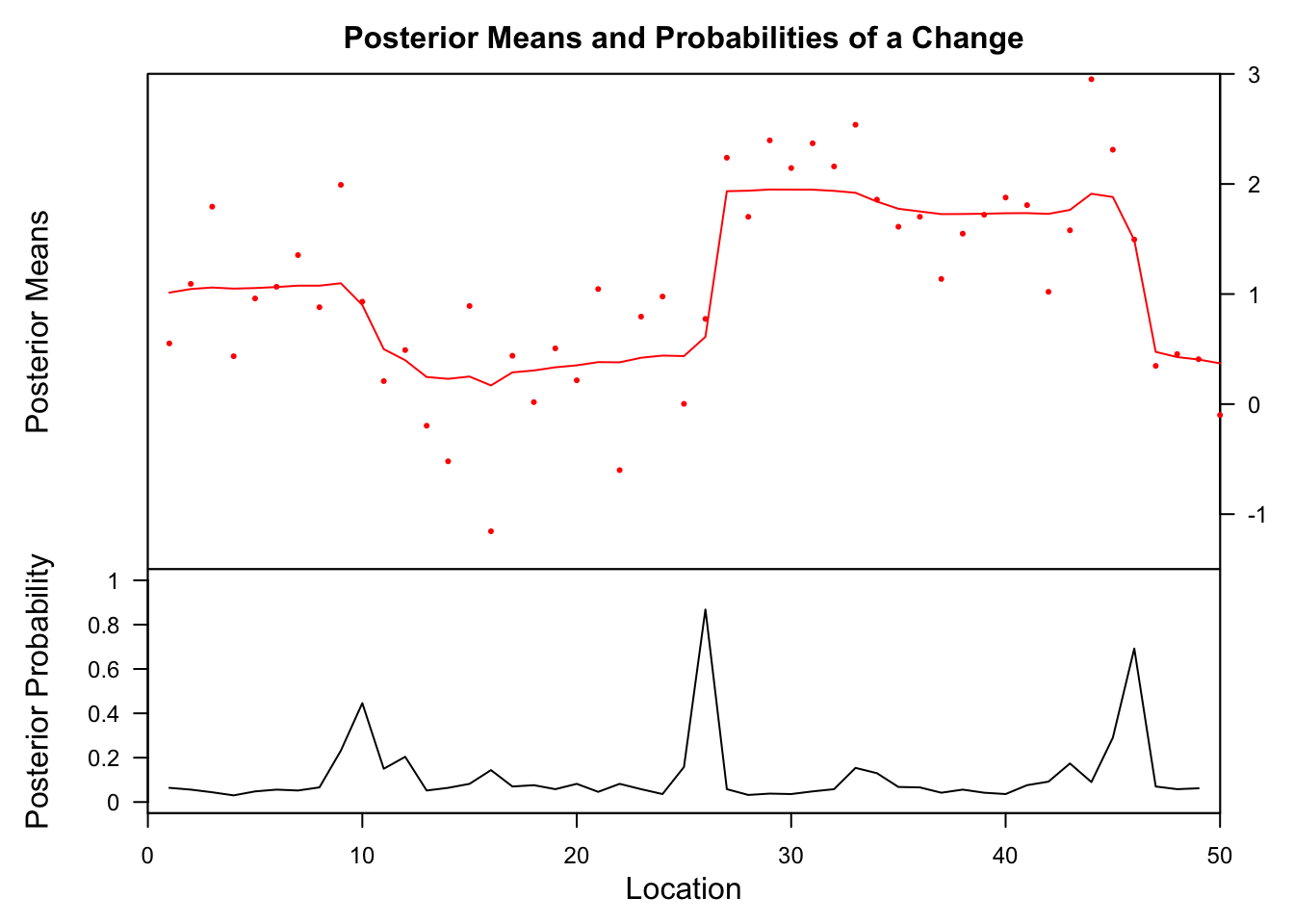
## Probability X1 id ## 26 0.868 0.6111902 26 The highest posterior probabilities for a modify are found at location 10, 26 and 46. Only only at #26 is the probability college so 70%, which is considered the minimum to indicate a significant modify.
strucchange
Generalized fluctuation test 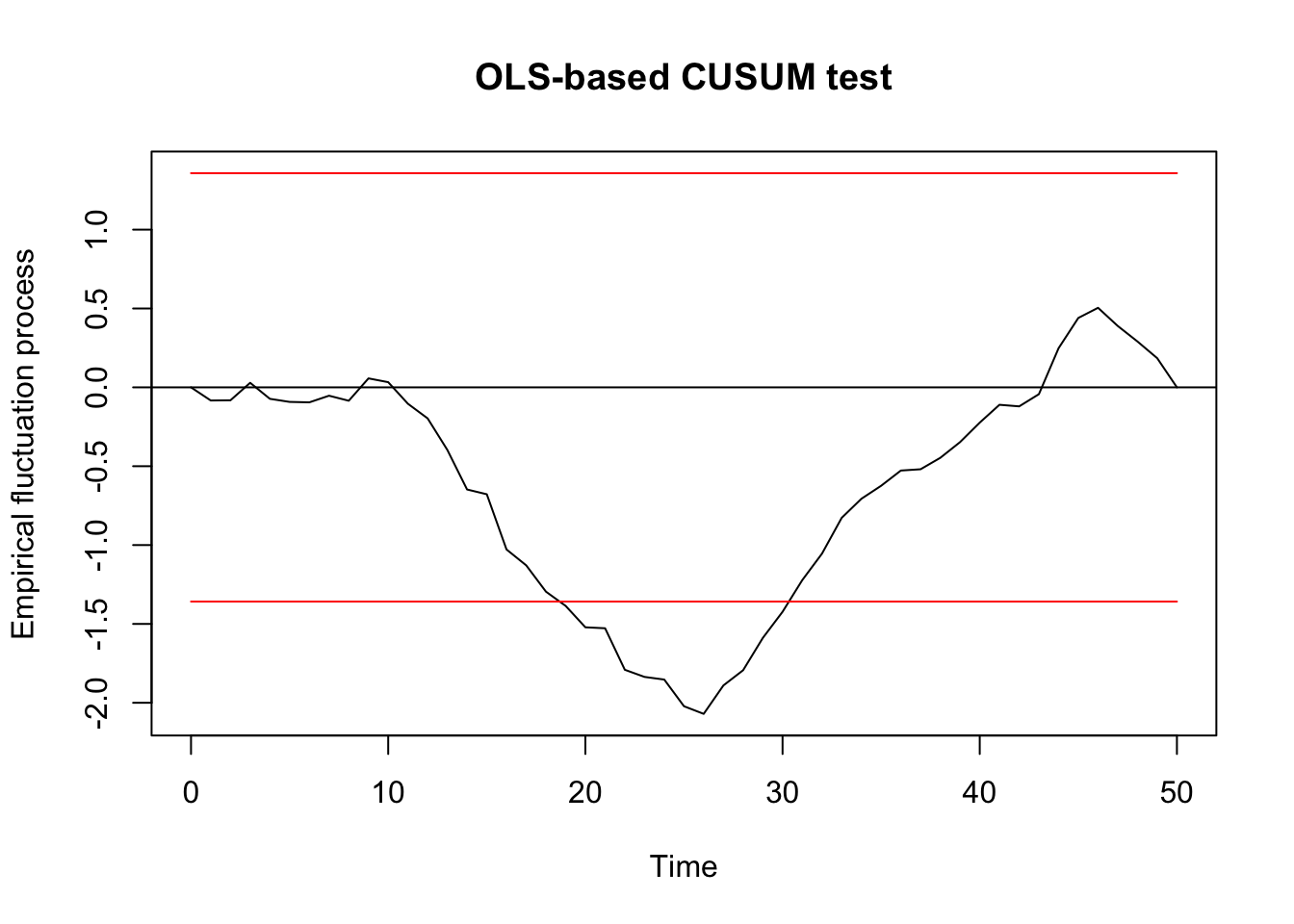
## ## OLS-based CUSUM examination ## ## data: ocus_mod ## S0 = 2.0704, p-value = 0.0003783 F test
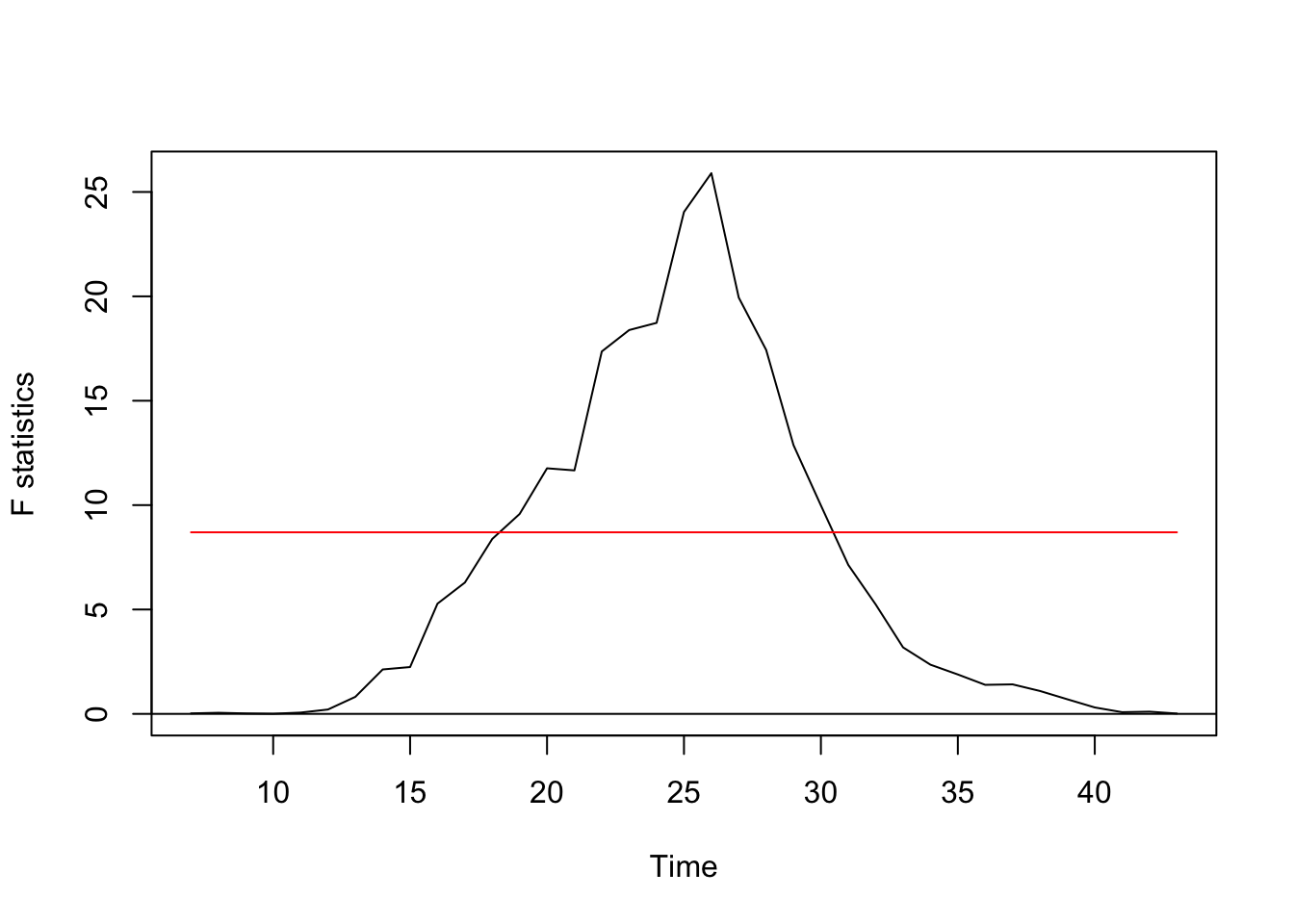
Regression breakpoints
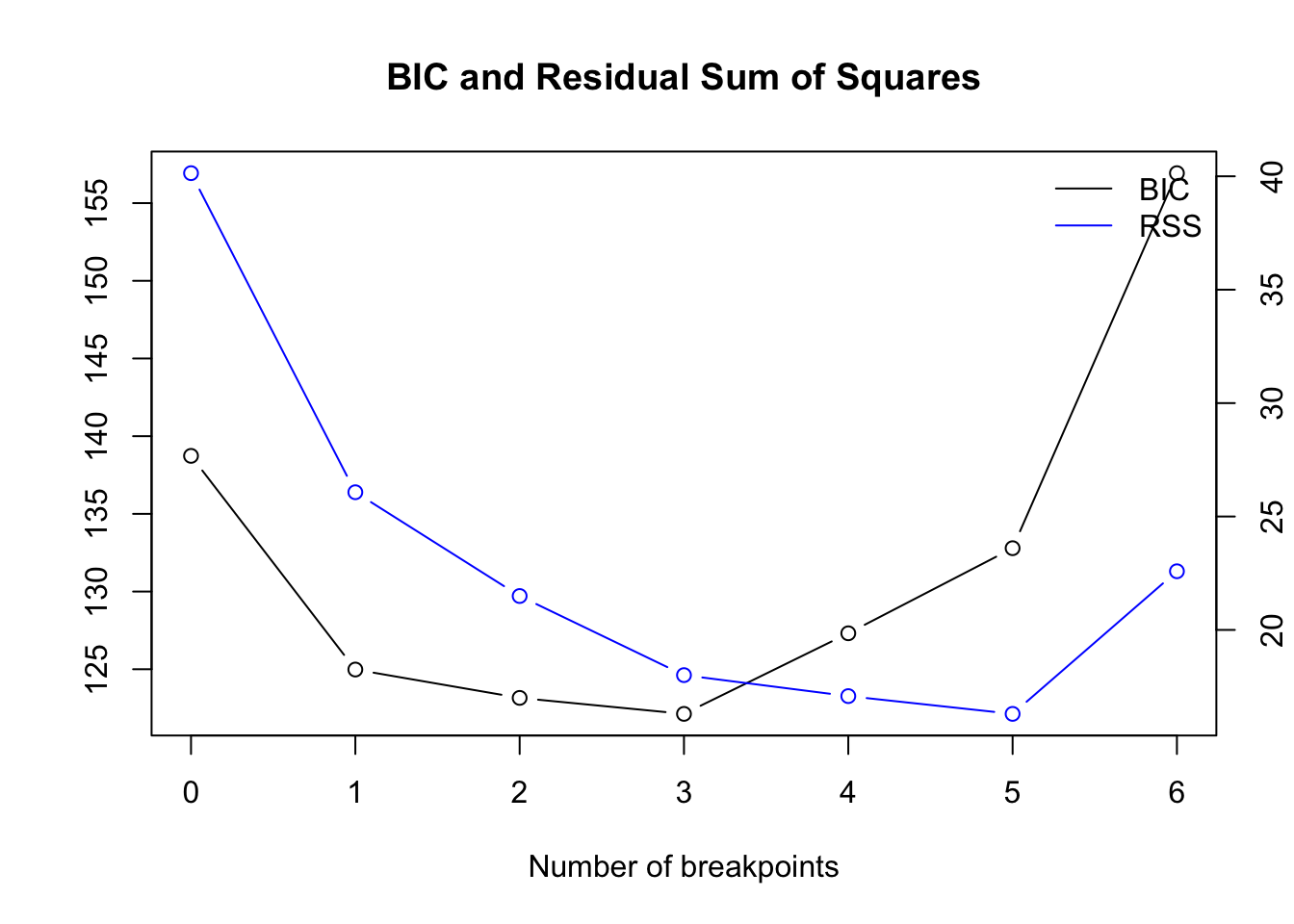
Optimal number of breakpoints:
## [1] iii Location of breakpoint:
## [one] x 26 34 While the first 2 frameworks detect merely one change indicate, the breakpoints analysis detects all 3 change points but with wider confidence interval:
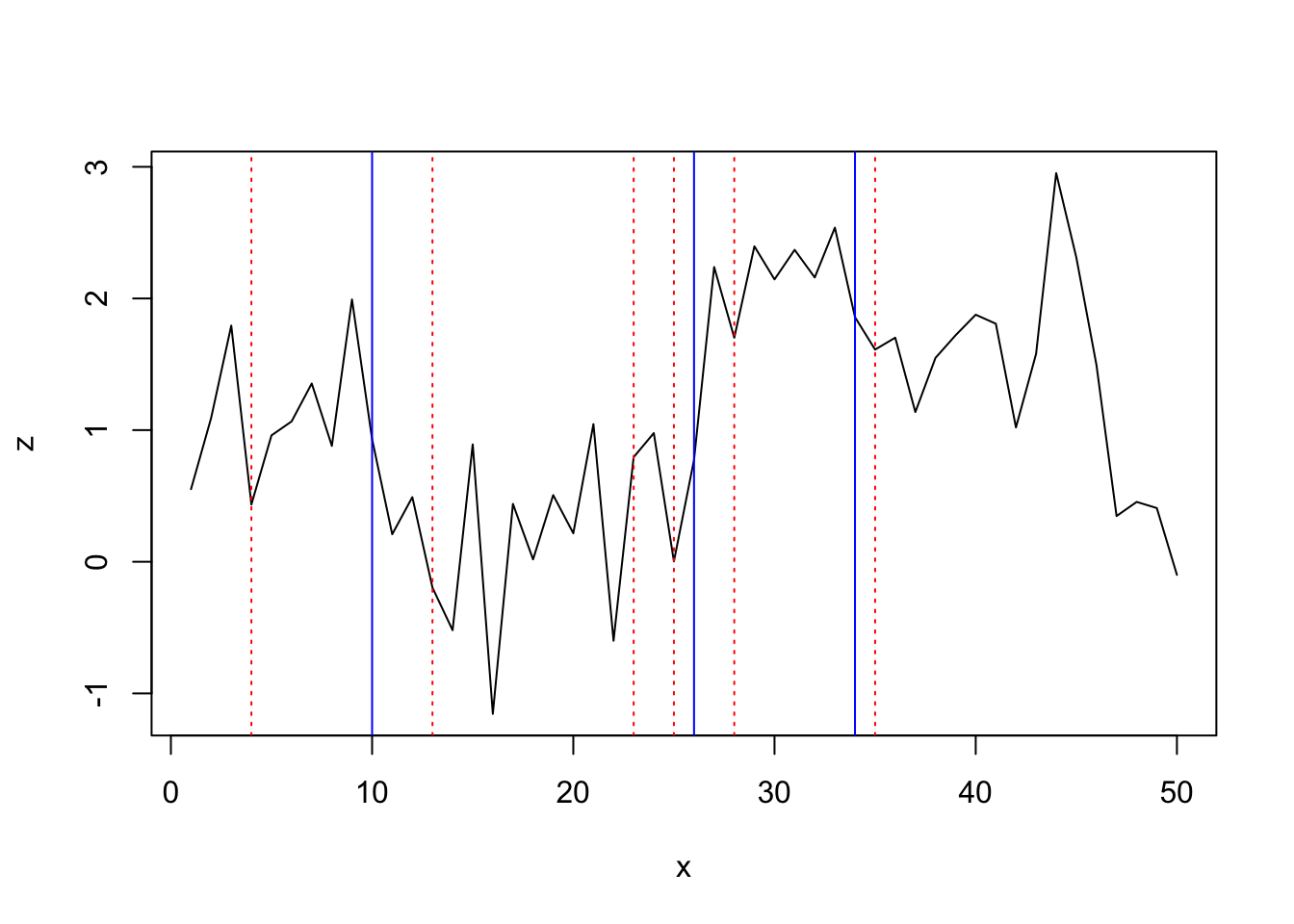
segmented
## Initial Est. St.Err ## psi1.x 20 44.99772 1.29978 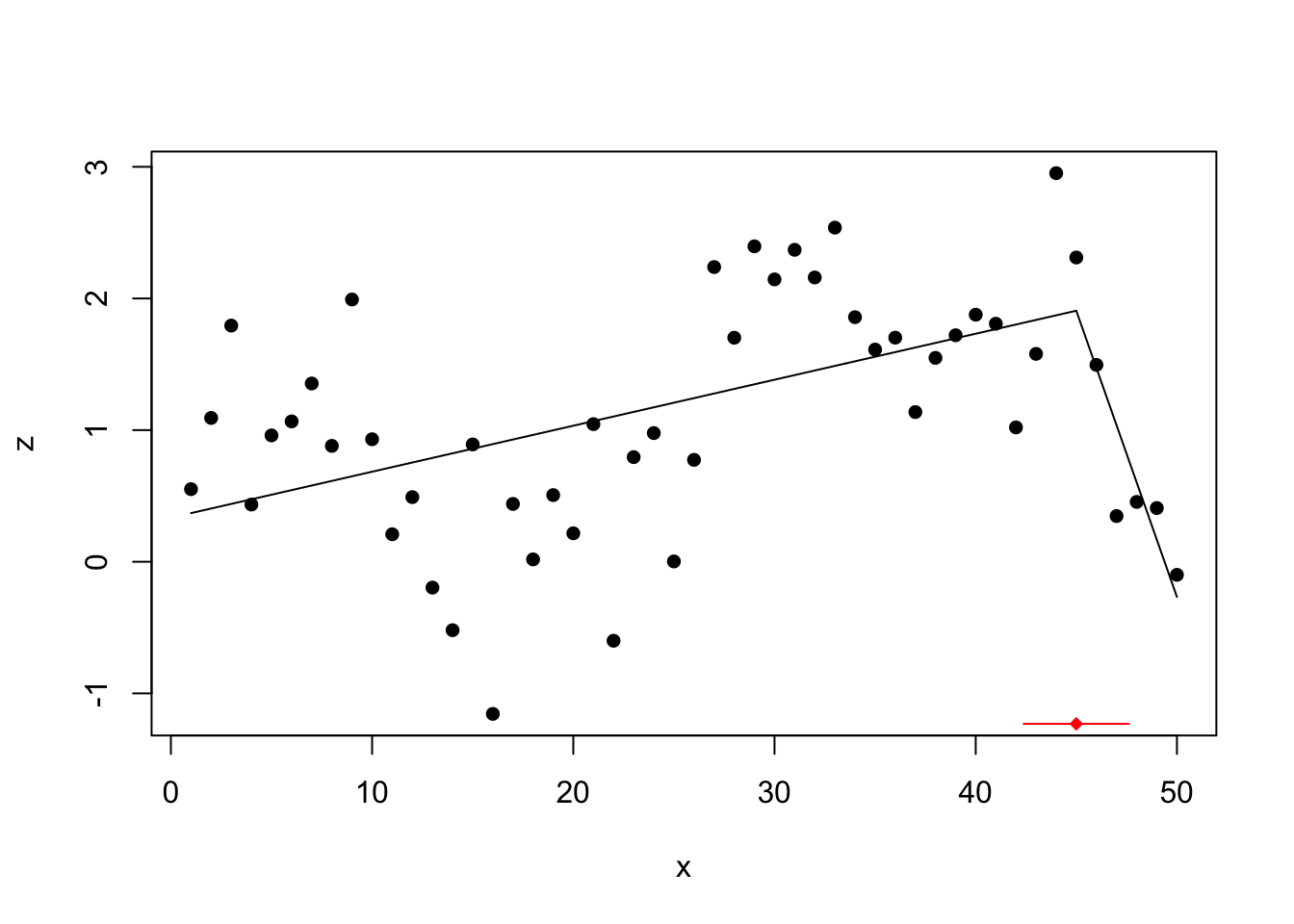
Only the final alter bespeak is found with this method.
tree
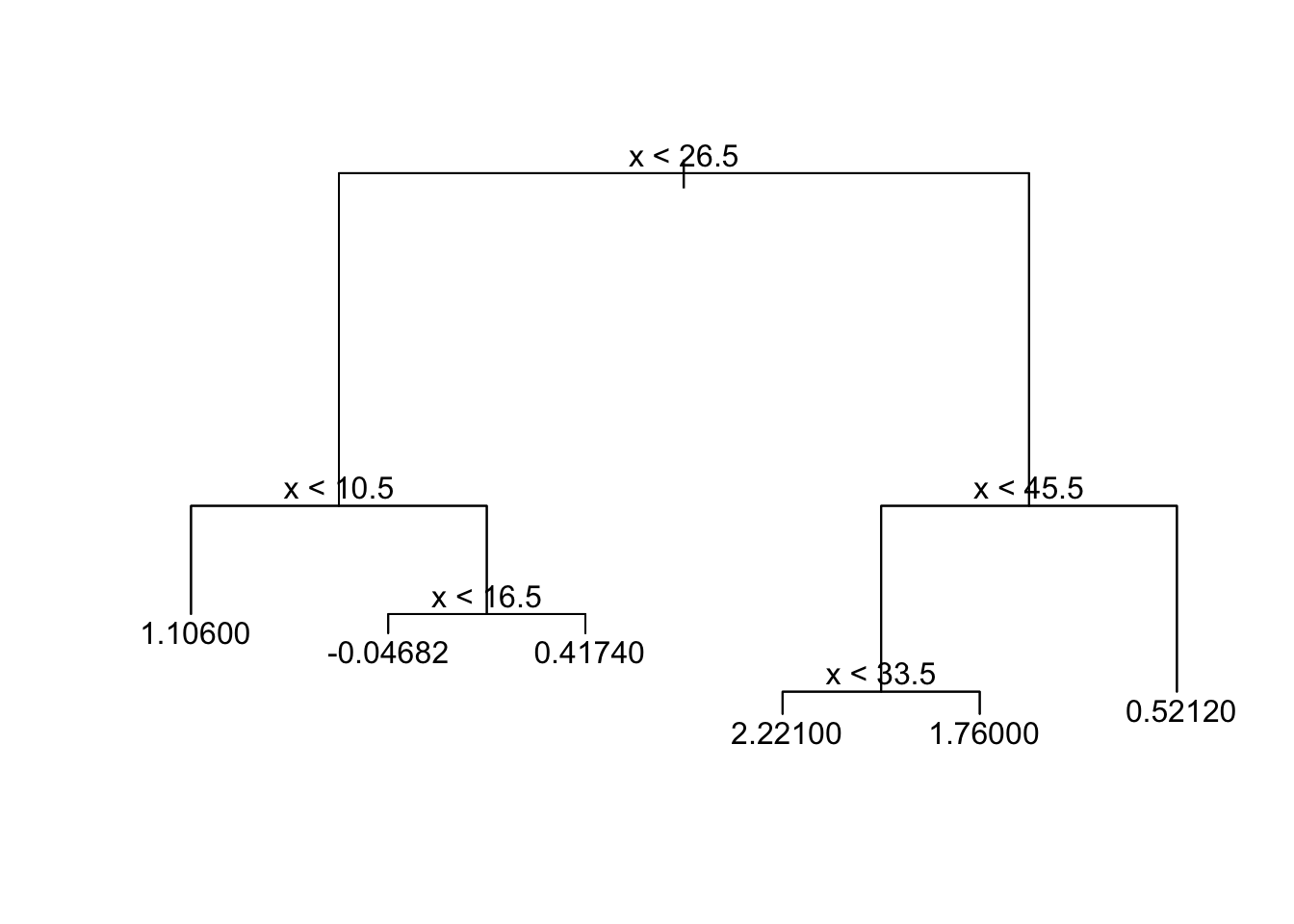
Linear human relationship (z~10) with ane break
gear up.seed(3) z <- numeric(20) ## Create showtime segment z[1:10] <- 20:11 + rnorm(x, 0, 1.v) ## Create second segment z[11:20] <- seq(11, fifteen, len=10) + rnorm(ten, 0, 1.v) df <- information.frame(ten = ane:20, z = z) plot(df$10, df$z, type='50',xlab='',ylab='') lines(x = 1:10,y = xx:xi, lwd = iii, col = 'red') lines(10 = xi:20, y = seq(11, 15, len=10), lwd = 3, col = 'red') 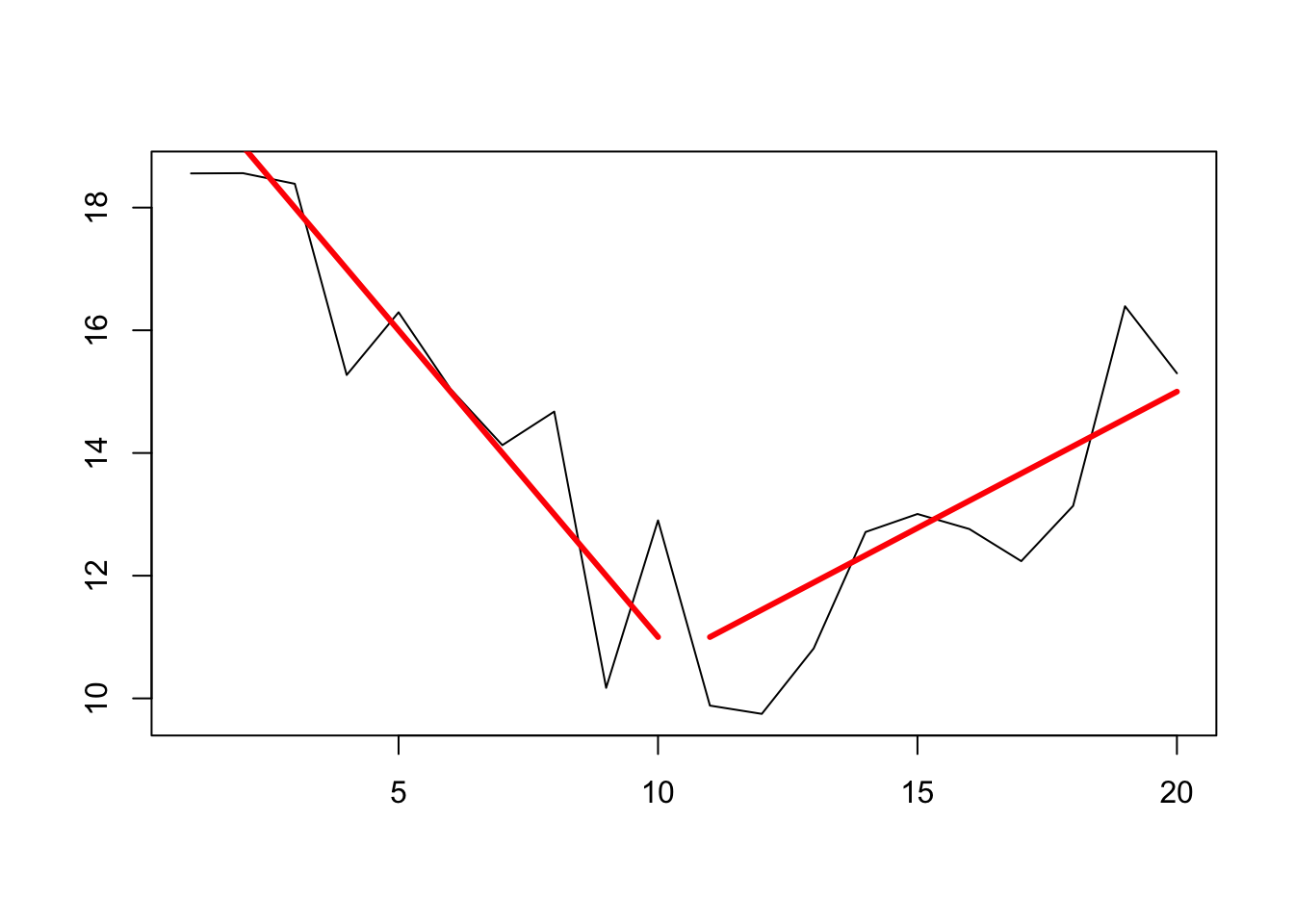
z_ts <- as.ts(df$z) (changepoints at 10/11)
changepoint
Testing for 1 change point in mean
## Created Using changepoint version ii.two.2 ## Changepoint type : Change in mean ## Method of analysis : AMOC ## Test Statistic : Normal ## Type of penalty : MBIC with value, 8.987197 ## Minimum Segment Length : 1 ## Maximum no. of cpts : 1 ## Changepoint Locations : 6 Testing for several using PELT method and AIC penalization:
## Course 'cpt' : Changepoint Object ## ~~ : S4 class containing 12 slots with names ## cpttype date version data.fix method exam.stat pen.type pen.value minseglen cpts ncpts.max param.est ## ## Created on : Friday Apr 26 xv:58:35 2019 ## ## summary(.) : ## ---------- ## Created Using changepoint version two.two.two ## Changepoint blazon : Change in mean ## Method of analysis : PELT ## Test Statistic : Normal ## Type of penalisation : AIC with value, 4 ## Minimum Segment Length : ane ## Maximum no. of cpts : Inf ## Changepoint Locations : 3 8 13 18 Testing for several using PELT method and CROPS penalty:
## [1] "Maximum number of runs of algorithm = viii" ## [1] "Completed runs = two" ## [1] "Completed runs = 3" ## [1] "Completed runs = 5" ## [i] "Completed runs = 6" ## [1] "Completed runs = 7" ## Created Using changepoint version 2.ii.2 ## Changepoint blazon : Change in mean ## Method of analysis : PELT ## Test Statistic : Normal ## Type of penalty : CROPS with value, 1 25 ## Minimum Segment Length : 1 ## Maximum no. of cpts : Inf ## Changepoint Locations : ## Number of segmentations recorded: 6 with between 1 and 7 changepoints. ## Penalty value ranges from: one to 24.57129 The diagnostic plot, yet, propose the model with 4 change points every bit nigh parsimonious:
plot(cpt2, diagnostic = TRUE) 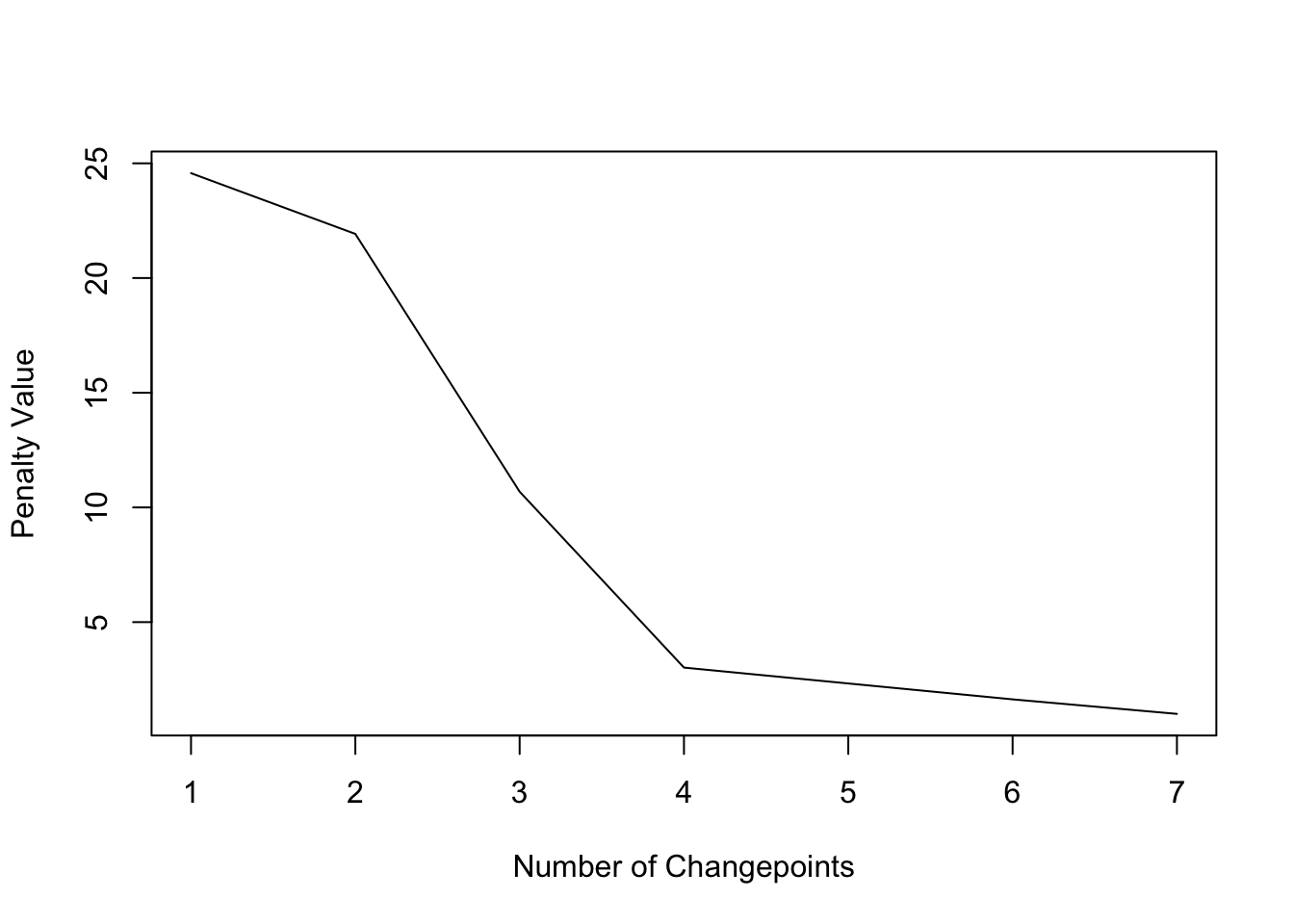
plot(cpt2, ncpts = 4) 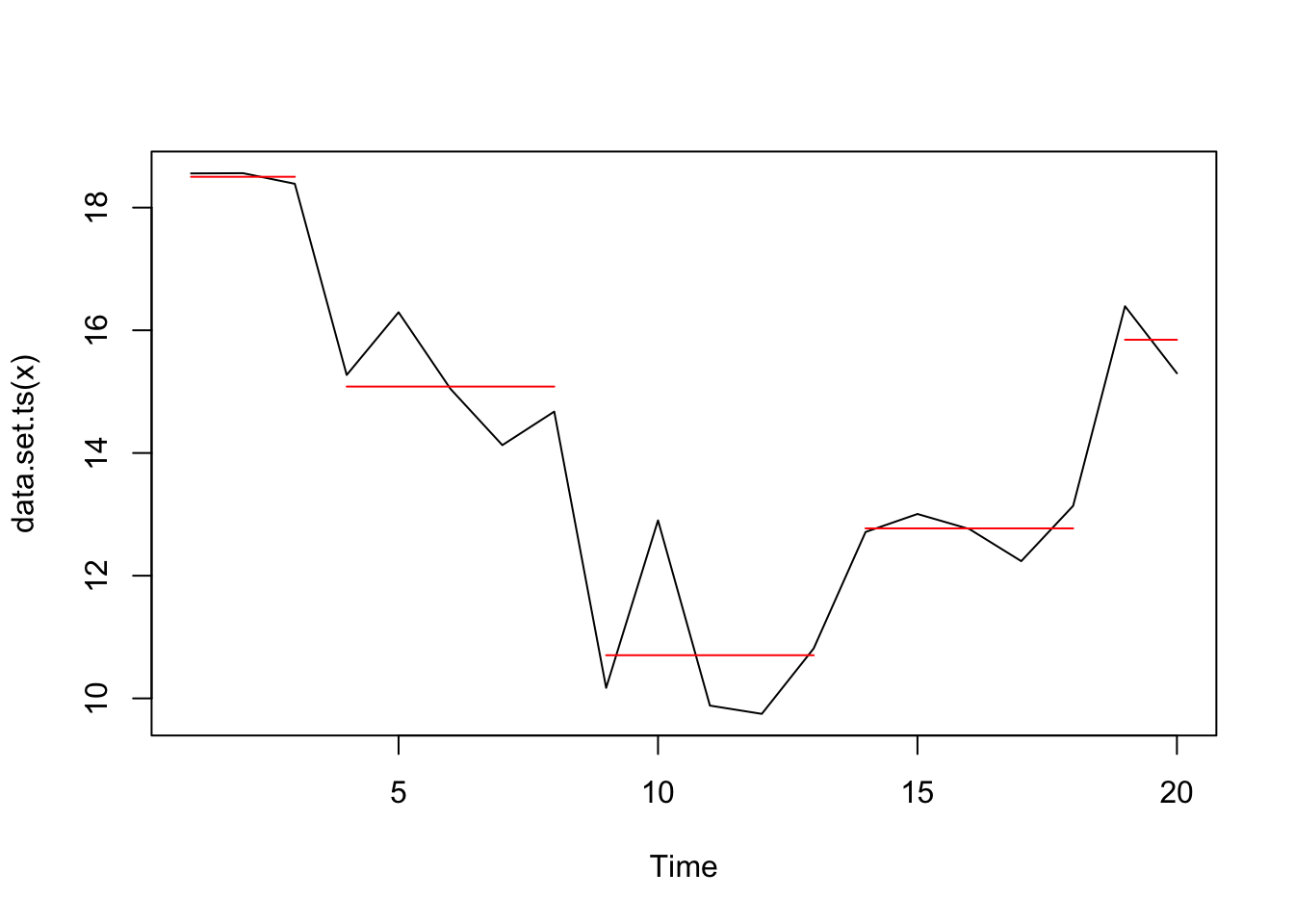
To get the exact locations i has to look at the full matrix of final models plant (by row) with their different number of modify points:
cpts.total(cpt2) ## [,1] [,2] [,3] [,4] [,5] [,6] [,7] ## [1,] iii 5 eight 9 10 13 18 ## [2,] 3 viii nine 10 13 18 NA ## [3,] 3 8 13 eighteen NA NA NA ## [iv,] 3 8 18 NA NA NA NA ## [5,] eight 18 NA NA NA NA NA ## [6,] 6 NA NA NA NA NA NA The model with only iv change points is row 3, and then the changepoints are at locations: 3, 8, 13, 18.
bcp
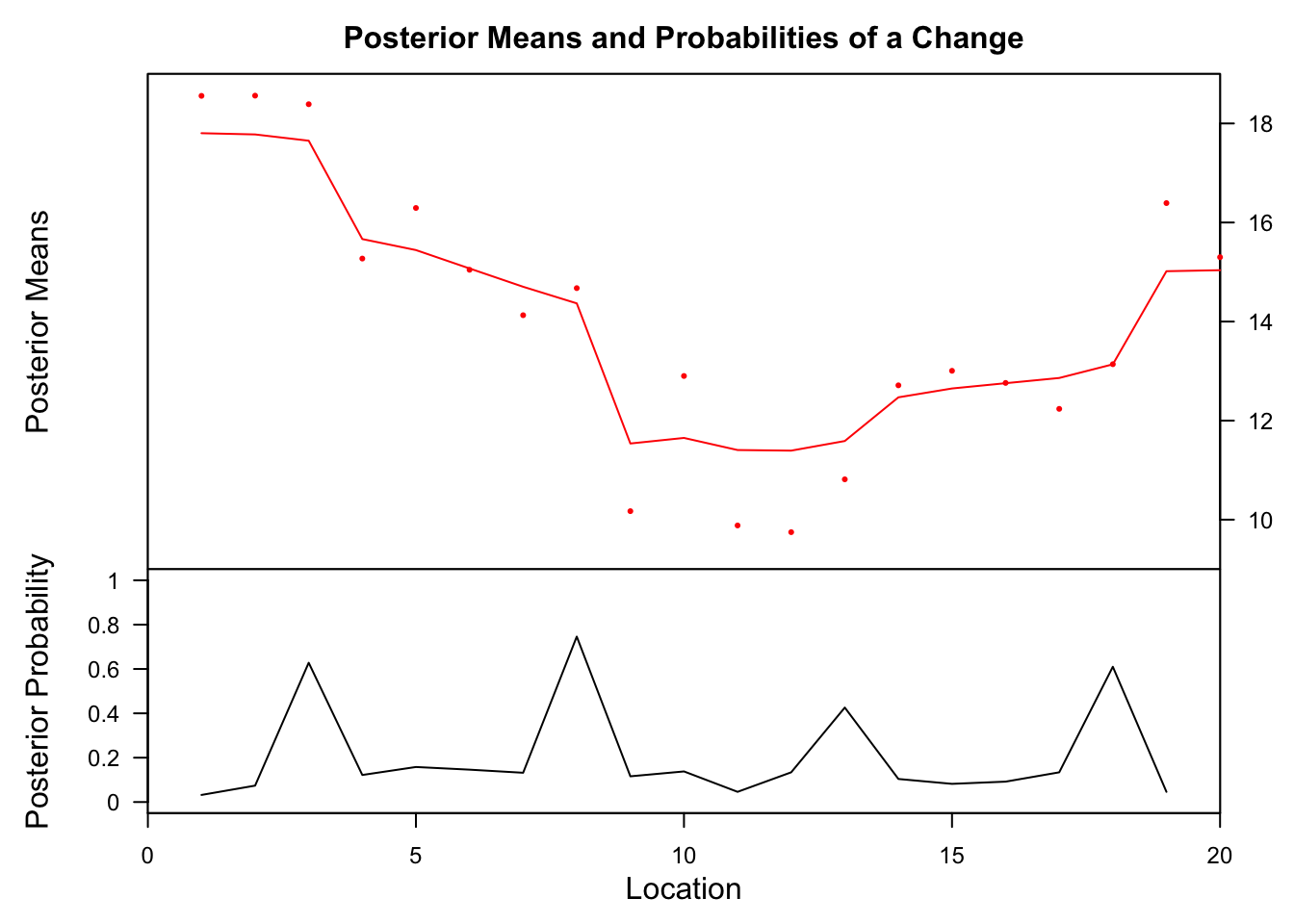
## Probability X1 id ## 8 0.746 xiv.36749 8 The bcp method finds a modify point at location eight, which is pretty shut to the true value.
strucchange
Generalized fluctuation test 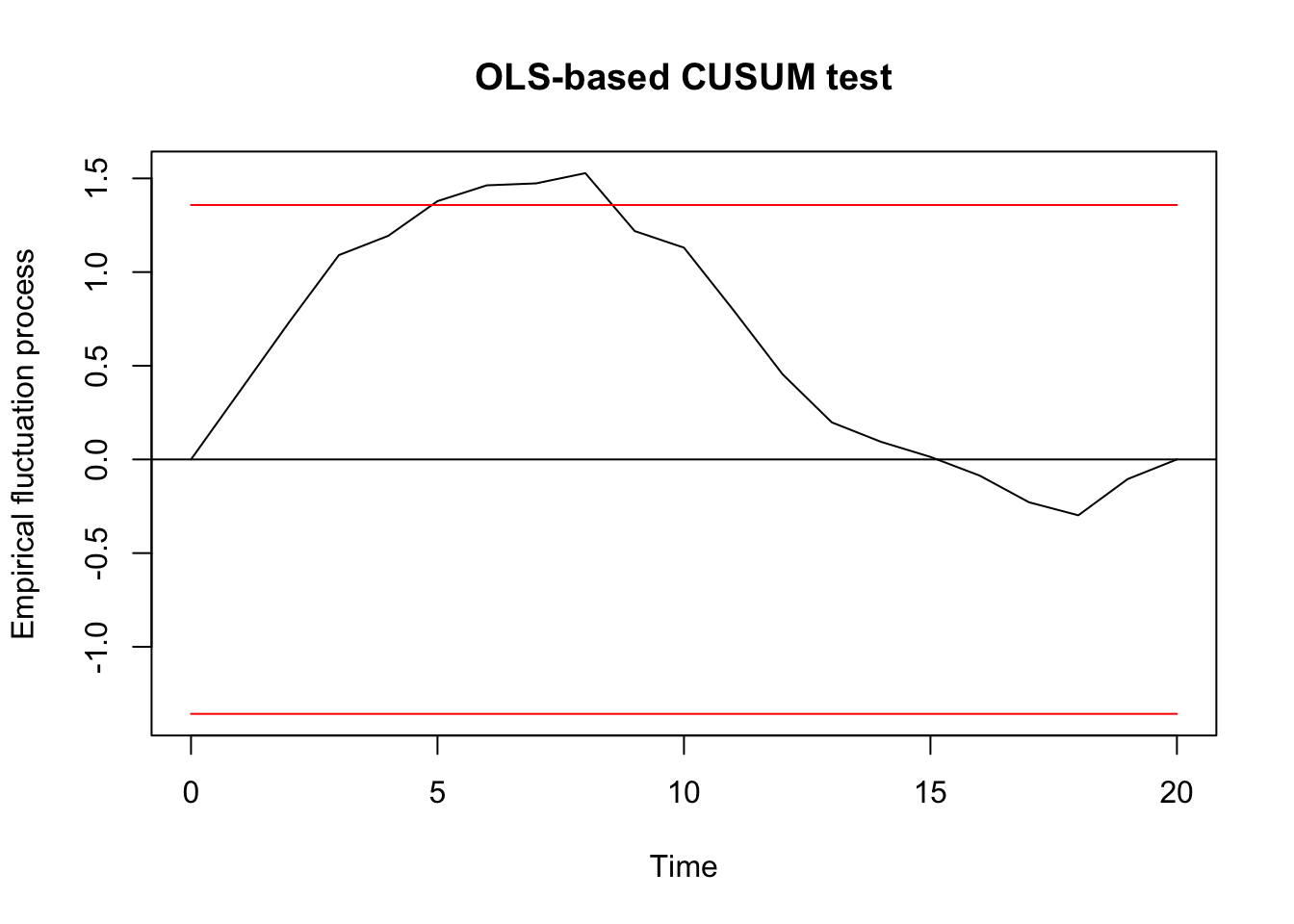
## ## OLS-based CUSUM test ## ## data: ocus_mod ## S0 = 1.528, p-value = 0.01876 F test
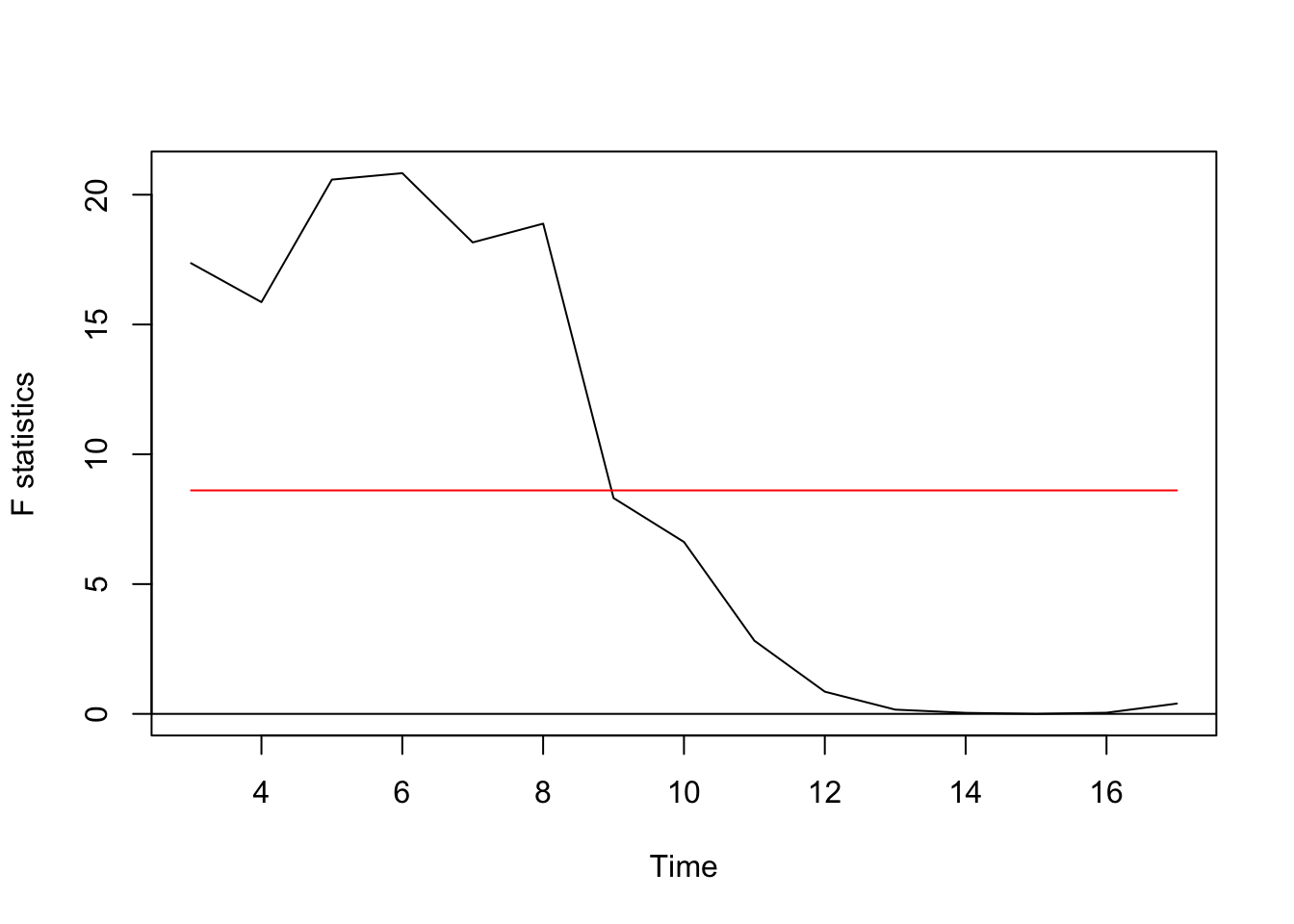
The pattern is less articulate here simply propose here optimal change points of vi.
Regression breakpoints
To test for changes in relationships the formula needs to be changed from z~1 to z~x:
bpts <- breakpoints(z ~ ten, data = df) 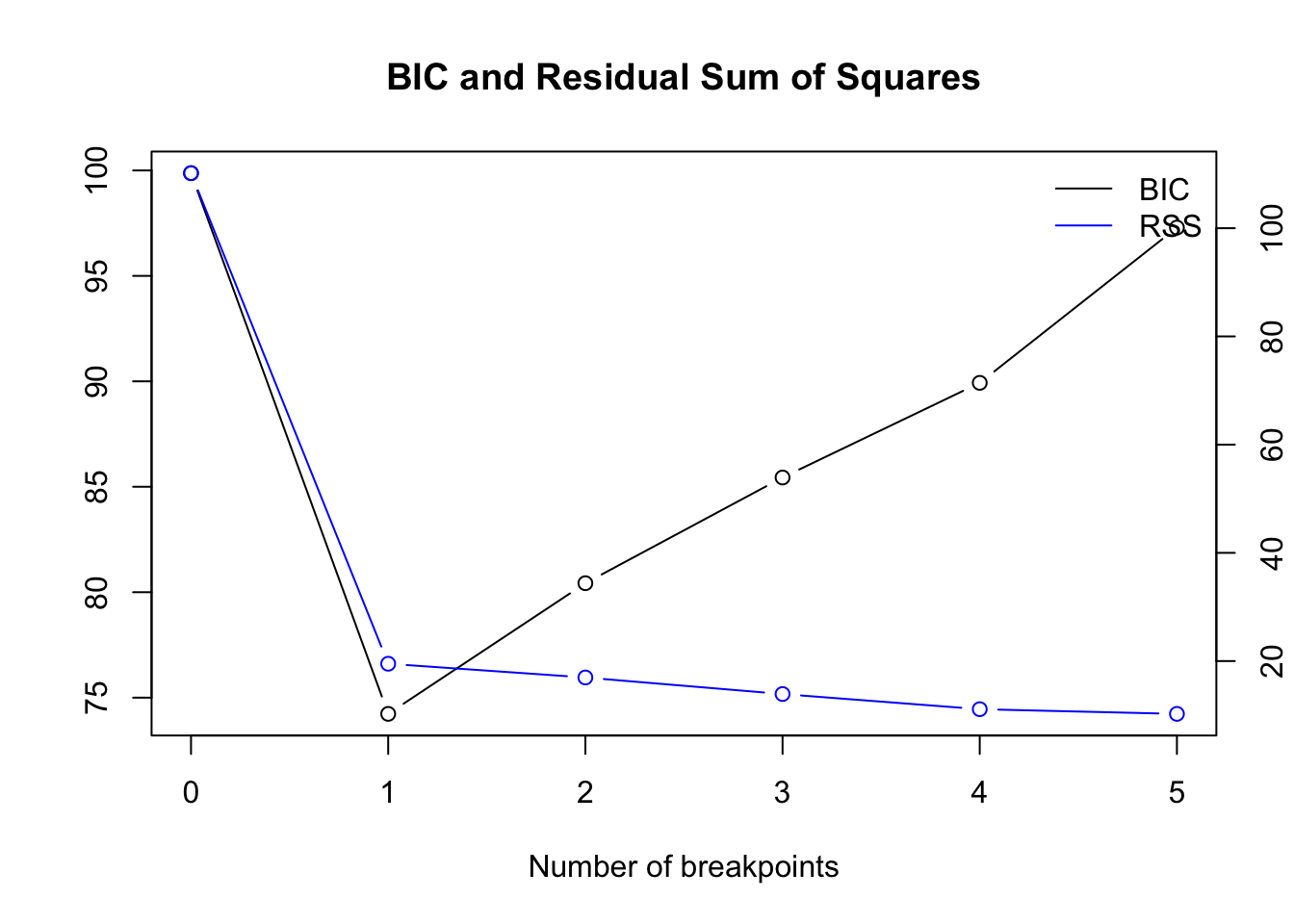
Optimal number of breakpoints:
## [one] one Location of breakpoint:
## [1] 10 While the first 2 frameworks detect NO change point, the breakpoints assay detects it exactly at location 10:
ci_mod <- confint(bpts, breaks = opt_brks) plot(z ~ ten, data = df, type = "l") for (i in 1: opt_brks) { abline(v = df$10[ci_mod$confint[i,2]], col = "blue") abline(five = df$ten[ci_mod$confint[i,i]], col = "red", lty = three) abline(v = df$ten[ci_mod$confint[i,iii]], col = "red", lty = three) } ## fit zip hypothesis model fm0 <- lm(z ~ x, data = df) # fit model with 1 breakpoint but formula dissimilar then in previous time serial: fm1 <- lm(z ~ x*(ten < best_brk) + ten*(x > best_brk), information = df) fm1_coef <- coef(fm1) fit1 <- (fm1_coef[1] + fm1_coef[3]) + (fm1_coef[two] + fm1_coef[five])*df$x[df$x <= best_brk] fit2 <- (fm1_coef[i] + fm1_coef[four]) + (fm1_coef[2])*df$x[df$10 >= best_brk] # add together to previous plot lines(df$10, fitted(fm0), col = 3) lines(df$x[1:best_brk], fit1, col = "orange") lines(df$x[best_brk:max(df$x)], fit2, col = "orangish") 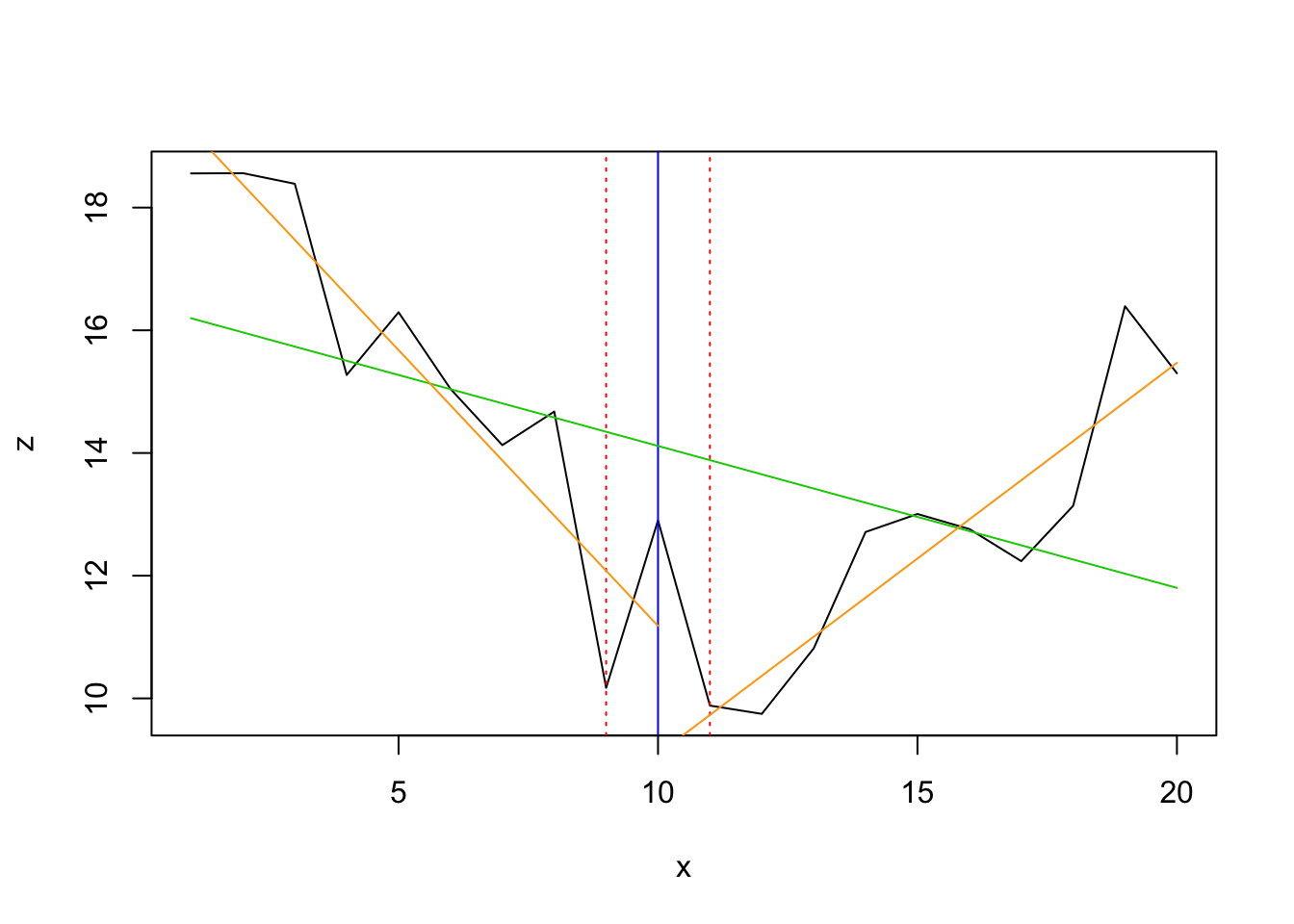
segmented
## Initial Est. St.Err ## psi1.10 x eleven.64798 0.6721446 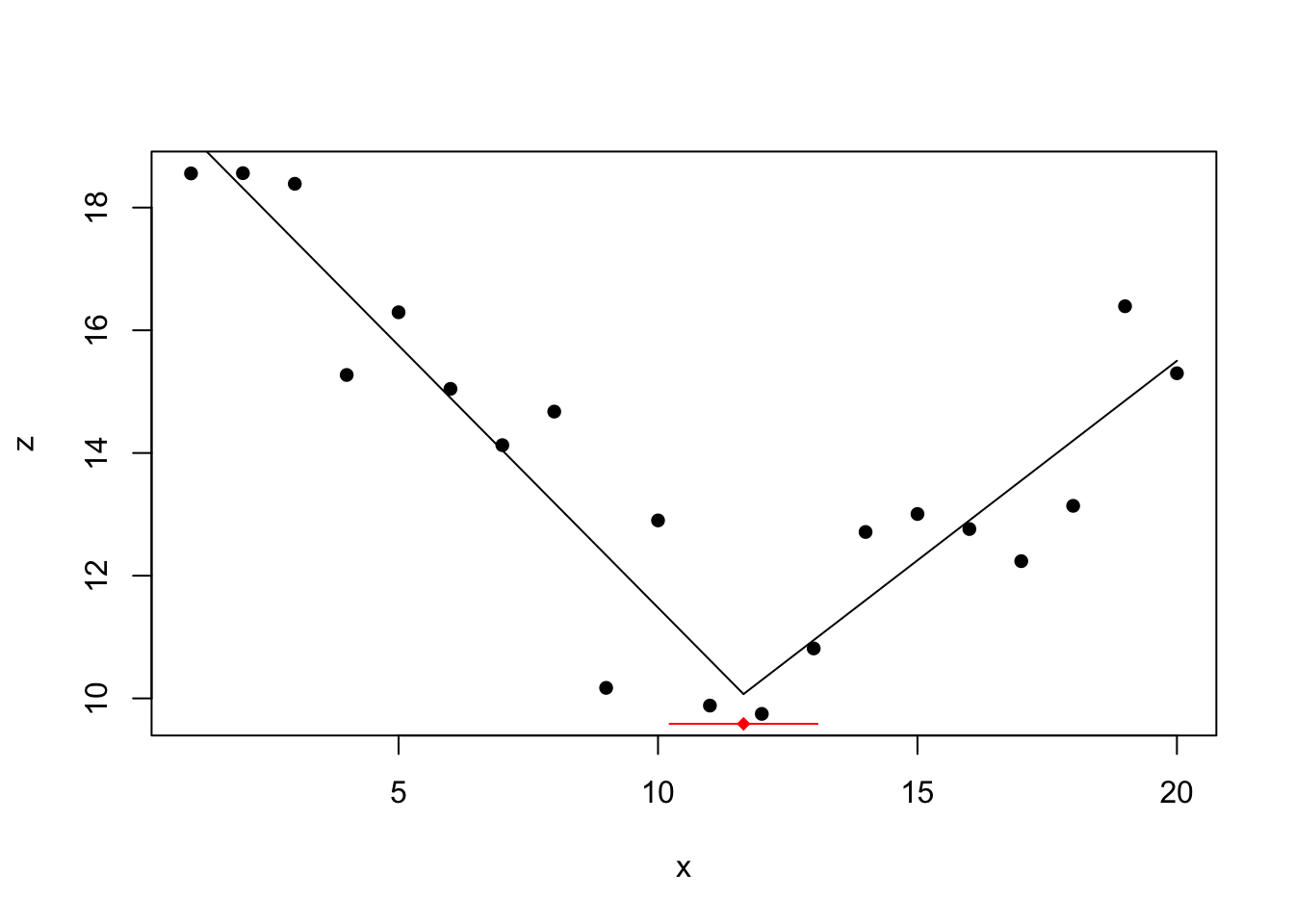
Also the segmented part detects correctly the change at location ten.
tree
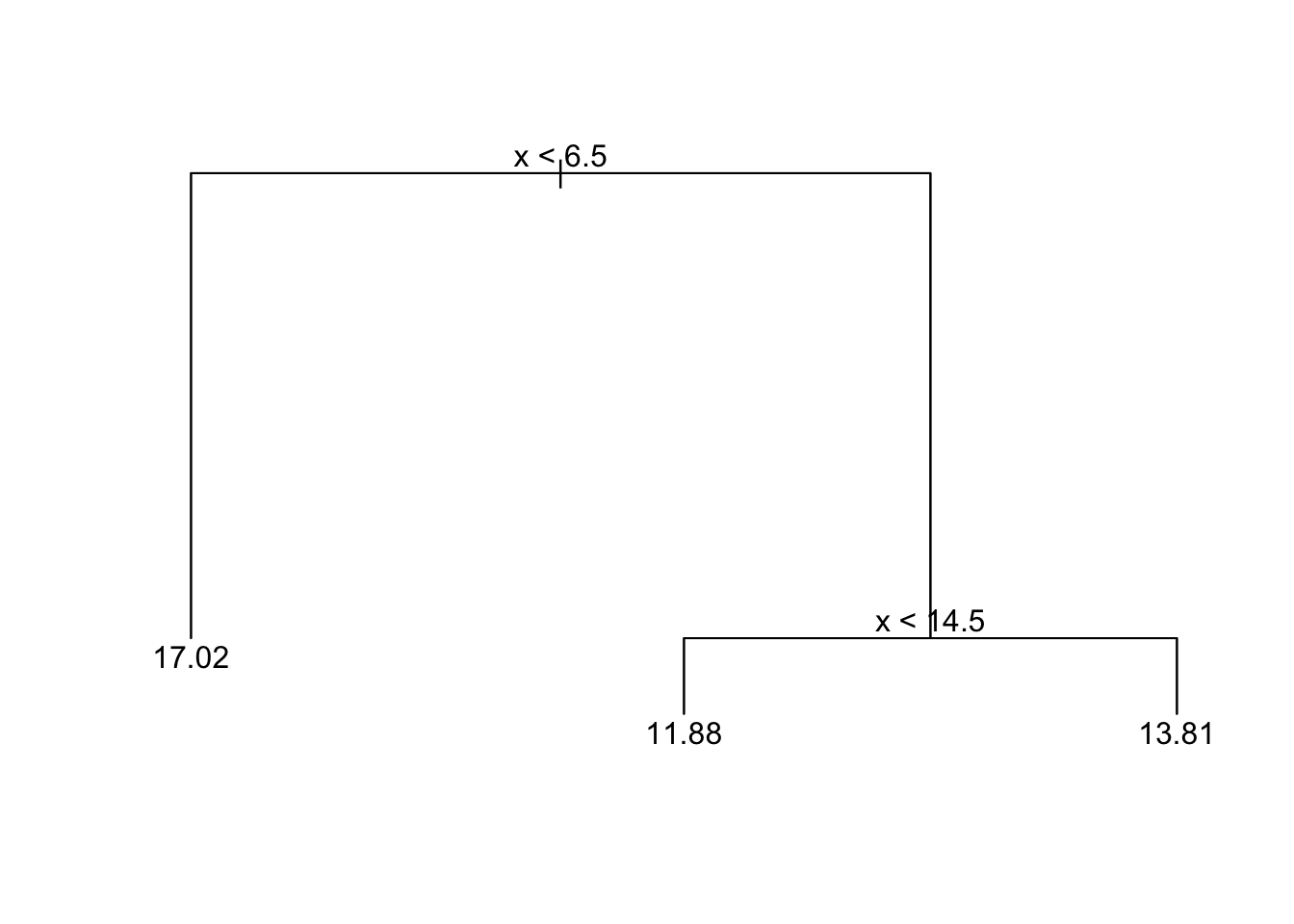
This tree methods detects 2 changes which are below and higher up the true change point.
Cubic disuse part (z~ten)
ready.seed(4) 10 <- one:50 z_nonoise <- (10000 + 0.05*ten + 0.2*x^2 - 0.ii*x^iii) z <- z_nonoise + rnorm(l,1000,500) df <- data.frame(x = x, z = z) plot(df$x, df$z, type = 'l', xlab = '', ylab = '') 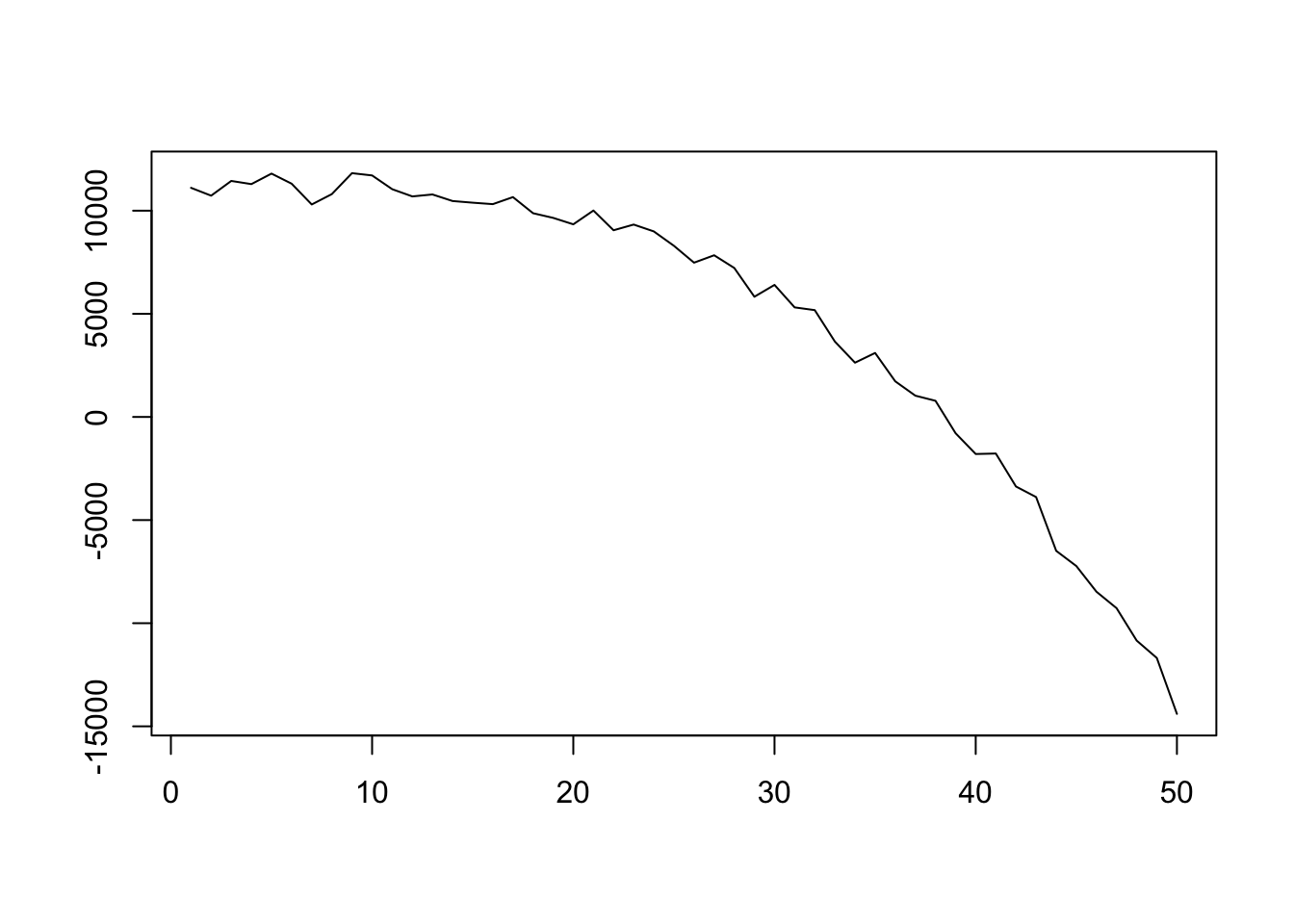
z_ts <- every bit.ts(df$z) changepoint
Testing for 1 alter indicate in mean
## Created Using changepoint version two.2.ii ## Changepoint type : Alter in mean ## Method of analysis : AMOC ## Exam Statistic : Normal ## Type of penalty : MBIC with value, 11.73607 ## Minimum Segment Length : one ## Maximum no. of cpts : 1 ## Changepoint Locations : 35 Testing for several using PELT method and AIC penalty:
## Form 'cpt' : Changepoint Object ## ~~ : S4 course containing 12 slots with names ## cpttype date version data.prepare method test.stat pen.type pen.value minseglen cpts ncpts.max param.est ## ## Created on : Friday April 26 15:58:35 2019 ## ## summary(.) : ## ---------- ## Created Using changepoint version 2.2.ii ## Changepoint type : Change in mean ## Method of analysis : PELT ## Test Statistic : Normal ## Type of penalisation : AIC with value, 4 ## Minimum Segment Length : 1 ## Maximum no. of cpts : Inf ## Number of changepoints: 49 Testing for several using PELT method and CROPS punishment:
## [1] "Maximum number of runs of algorithm = 2" ## [ane] "Completed runs = two" ## Created Using changepoint version 2.2.ii ## Changepoint blazon : Change in hateful ## Method of analysis : PELT ## Test Statistic : Normal ## Blazon of penalisation : CROPS with value, 1 25 ## Minimum Segment Length : one ## Maximum no. of cpts : Inf ## Changepoint Locations : ## Range of segmentations: ## [,ane] [,2] [,3] [,4] [,five] [,half dozen] [,seven] [,8] [,9] [,10] [,11] [,12] [,xiii] ## [1,] 1 2 iii four 5 6 7 8 9 10 11 12 xiii ## [,xiv] [,xv] [,16] [,17] [,18] [,19] [,xx] [,21] [,22] [,23] [,24] ## [1,] 14 15 16 17 xviii 19 20 21 22 23 24 ## [,25] [,26] [,27] [,28] [,29] [,thirty] [,31] [,32] [,33] [,34] [,35] ## [one,] 25 26 27 28 29 30 31 32 33 34 35 ## [,36] [,37] [,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] ## [1,] 36 37 38 39 twoscore 41 42 43 44 45 46 ## [,47] [,48] [,49] ## [1,] 47 48 49 ## ## For penalisation values: ane Nothing detected.
bcp
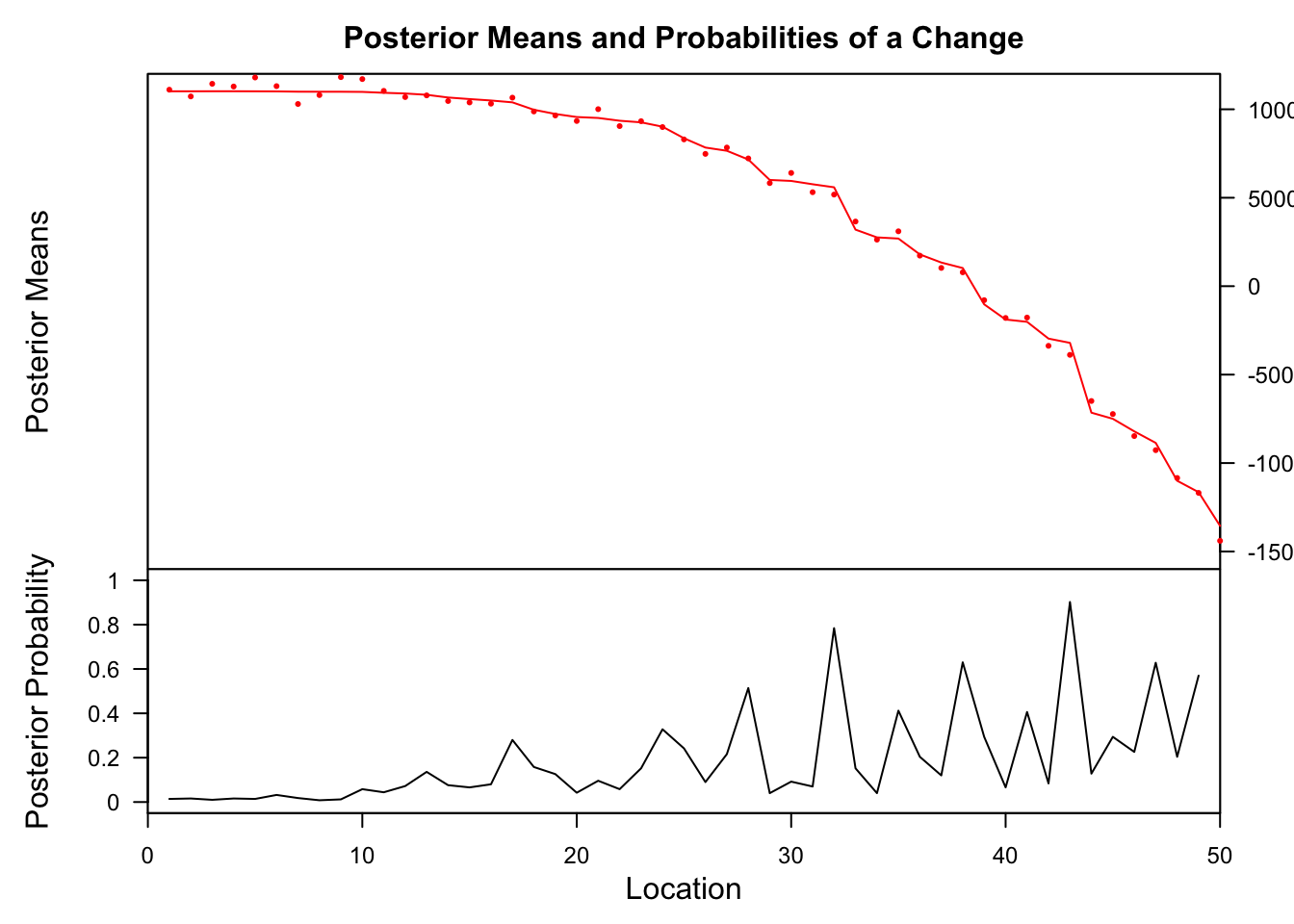
## Probability X1 id ## 32 0.784 5591.184 32 ## 43 0.902 -3204.395 43 strucchange
Generalized fluctuation test 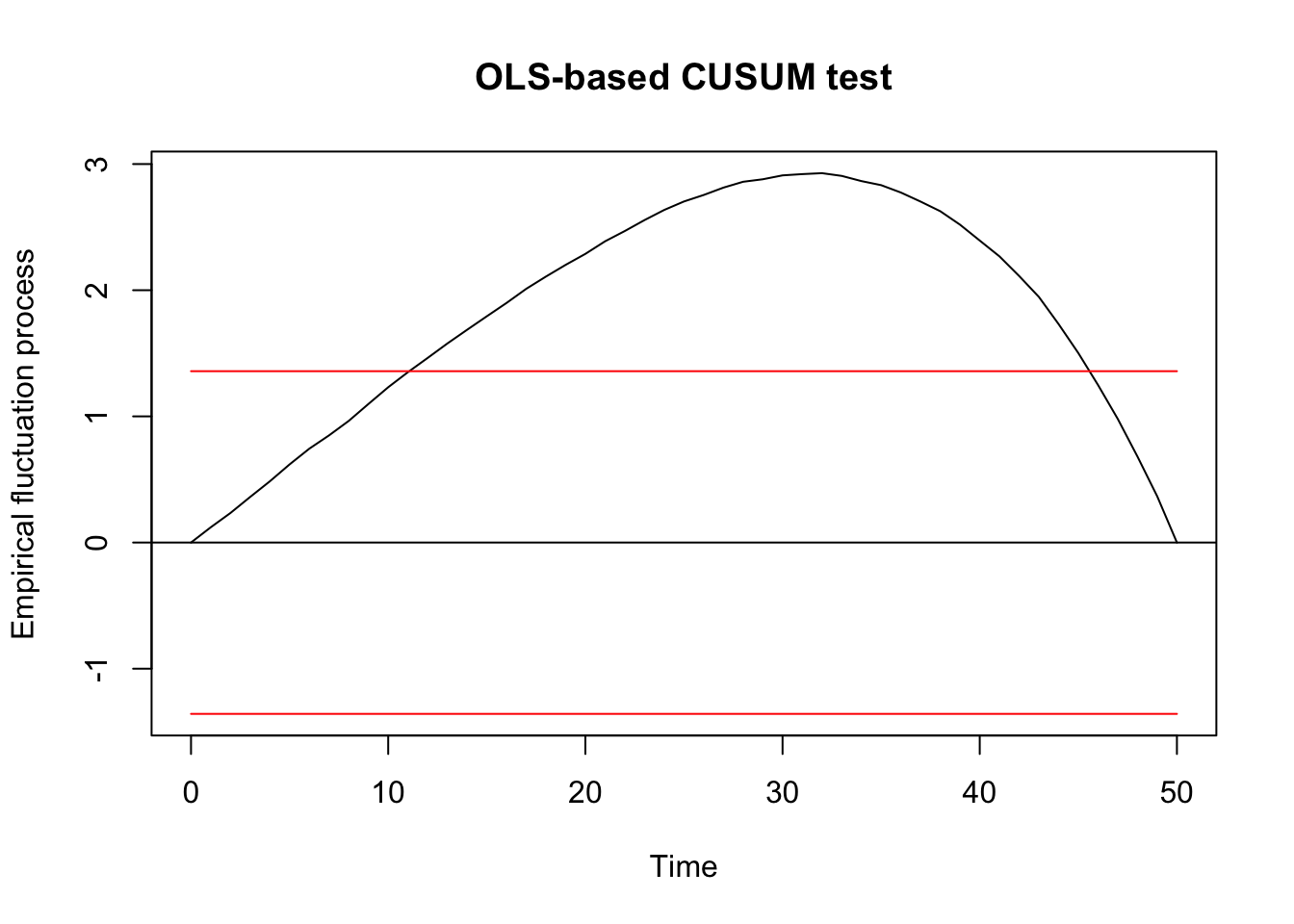
## ## OLS-based CUSUM exam ## ## data: ocus_mod ## S0 = 2.9277, p-value = 7.175e-08 F exam
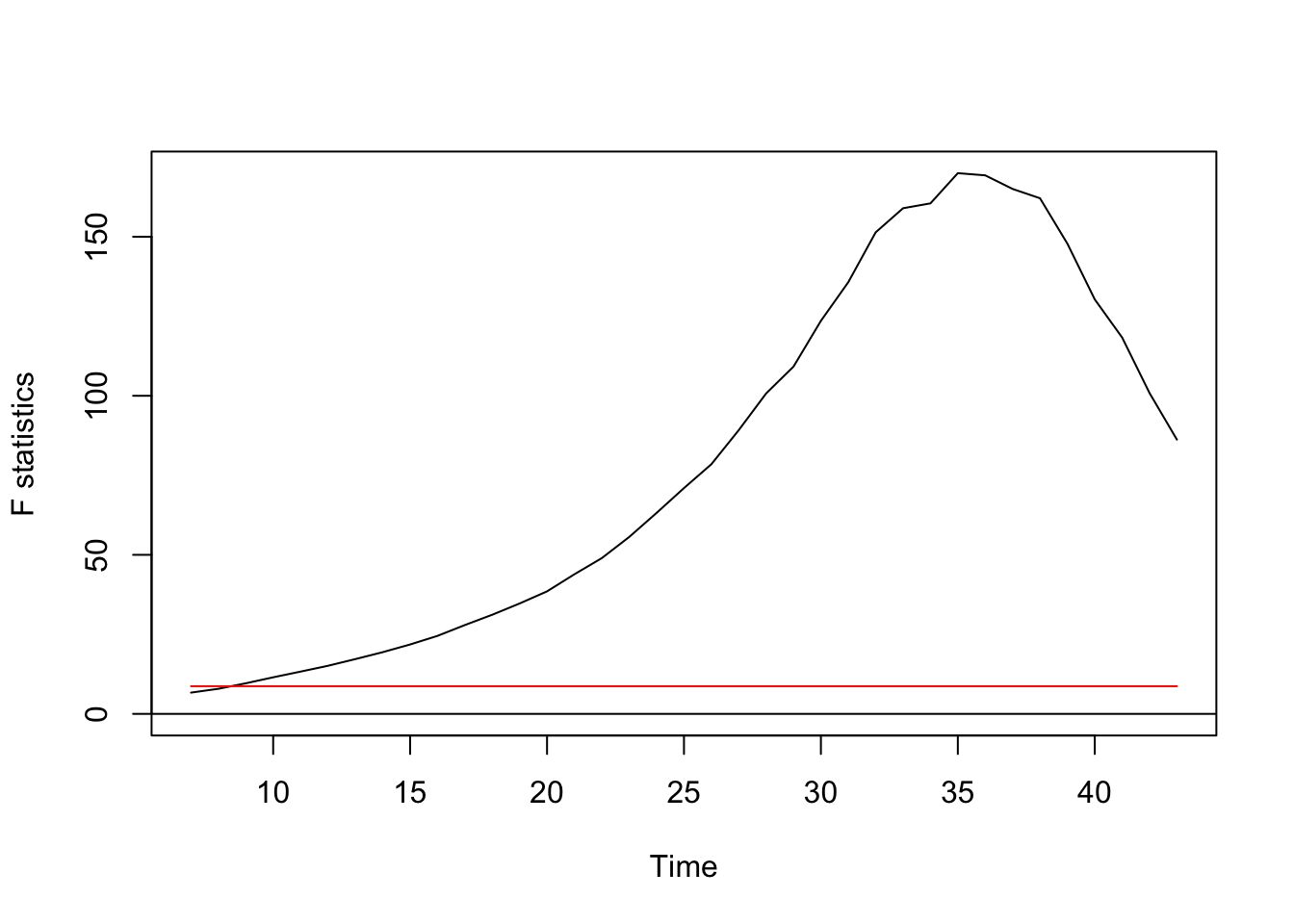
Regression breakpoints
Optimal number of breakpoints:
## [1] 3 Location of breakpoint:
## [1] 8 26 41 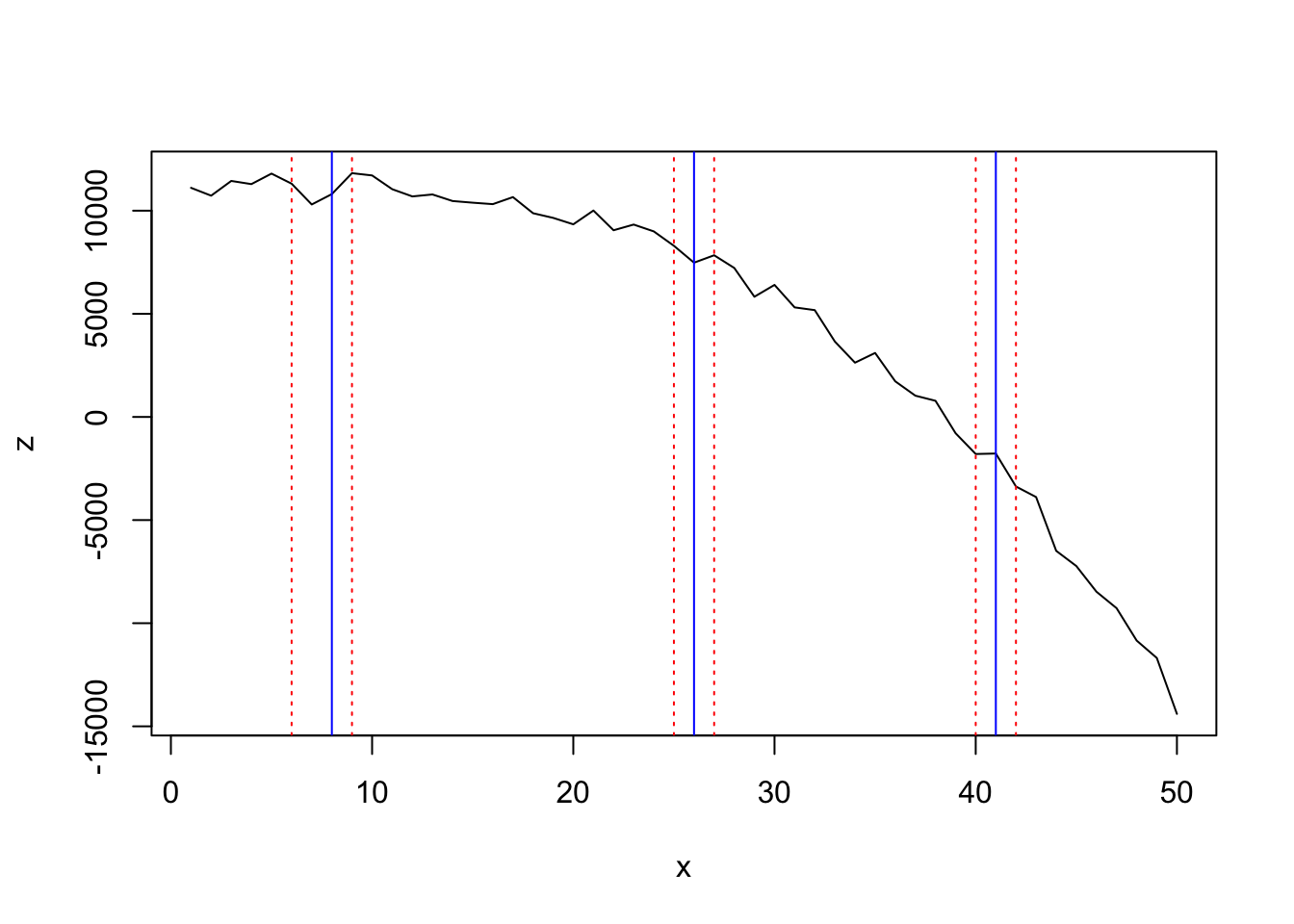
segmented
## Initial Est. St.Err ## psi1.10 10 29.67403 0.579635 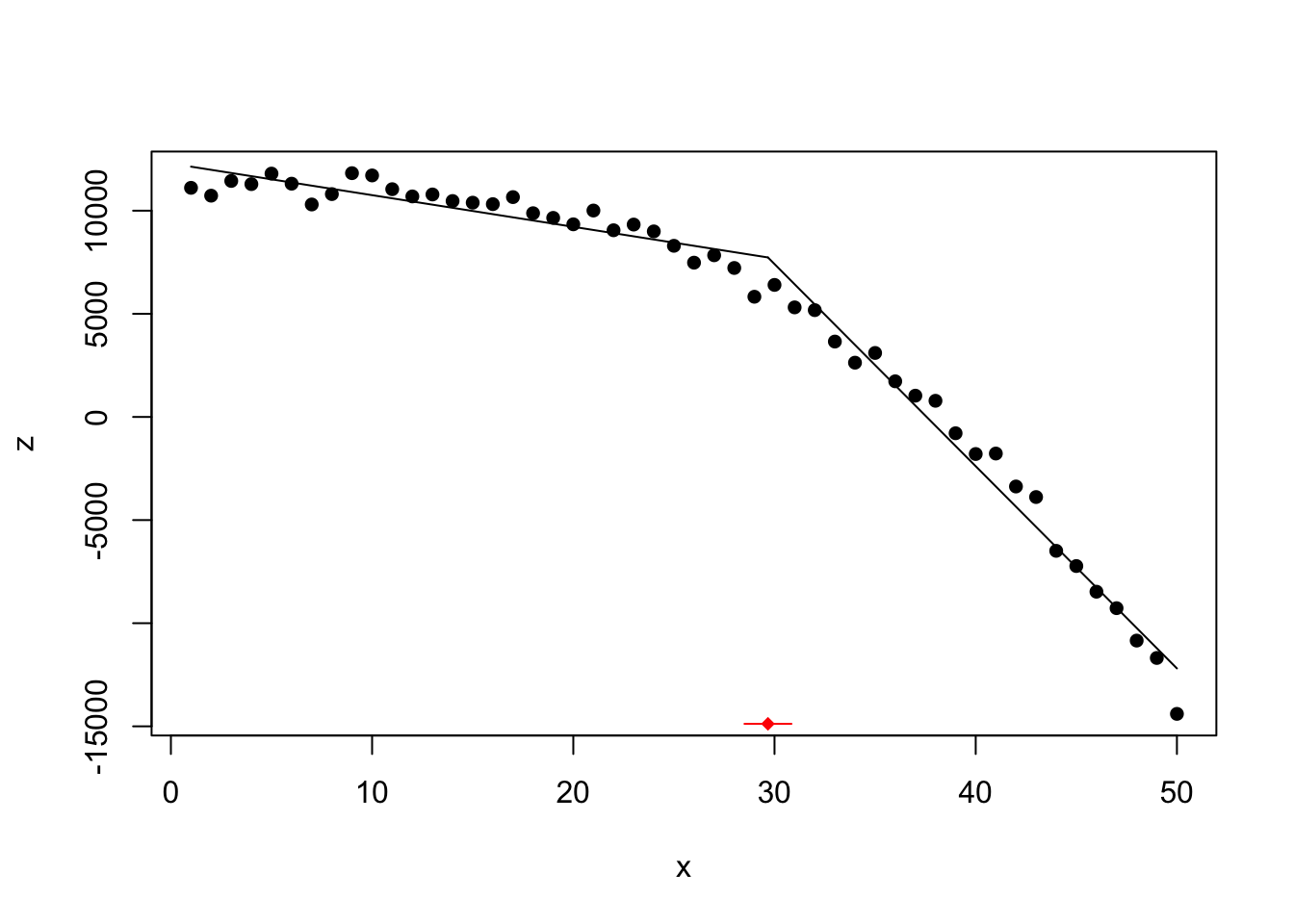
tree
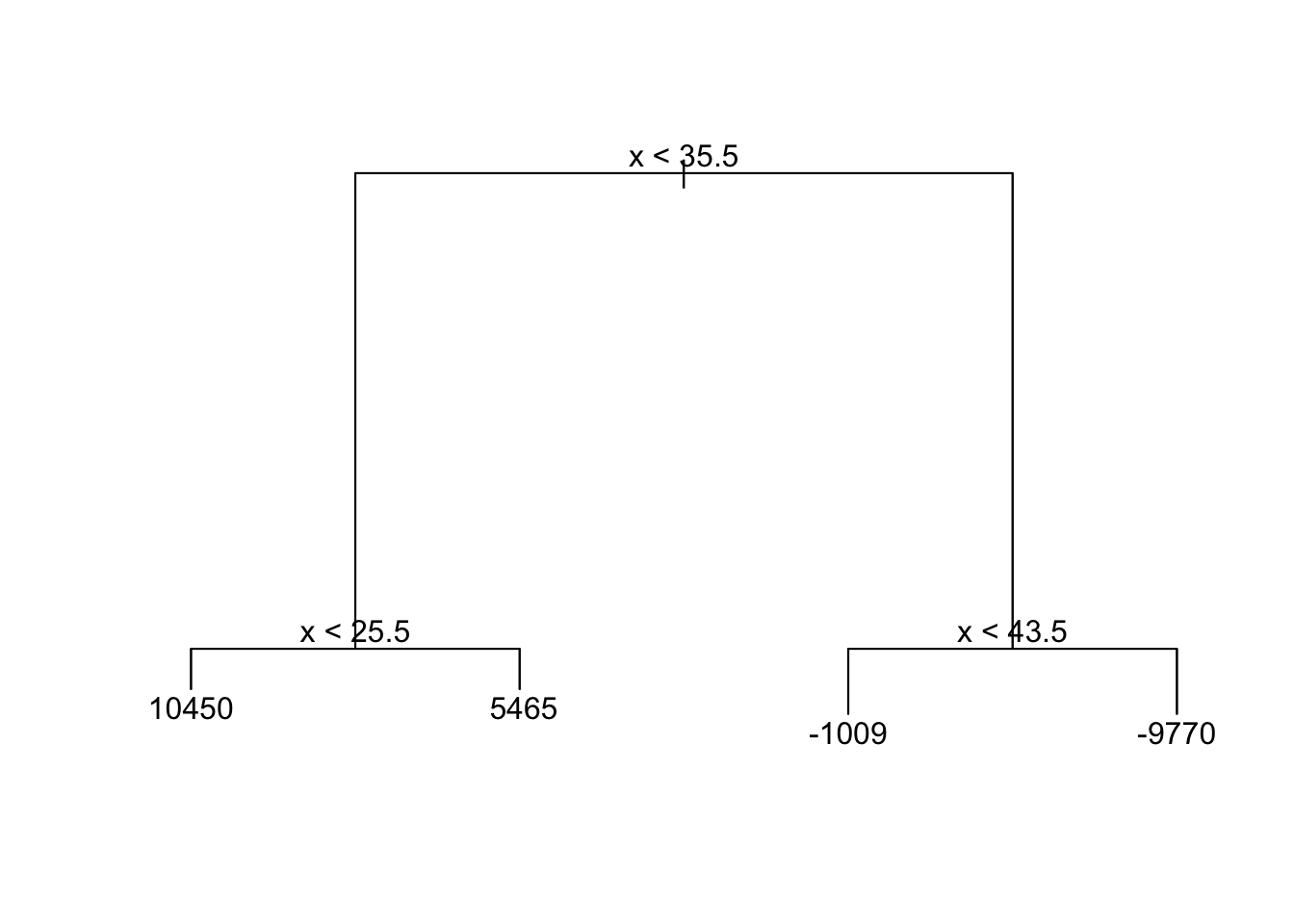
Highly non-linear (three changes in regression)
set.seed(5) x <- ane:50 z_nonoise <- c(0.1*ten[one:10], i.five-0.2*(x[11:25]-11), -ane.5 + 0.2*(ten[26:45]-26), rep(1,v)) z <- z_nonoise + rnorm(50,0,0.two) df <- data.frame(10 = ten, z = z) plot(df$x, df$z, type = 'l', xlab = '', ylab = '') lines(ten = one:ten,y = 0.1*x[1:10], lwd = 3, col = 'cerise') lines(x = eleven:25, y = 1.five-0.two*(x[11:25]-11), lwd = three, col = 'red') lines(x = 26:45, y = -1.5 + 0.2*(x[26:45]-26), lwd = 3, col = 'red') lines(x = 46:fifty, y = rep(1,5), lwd = three, col = 'red') 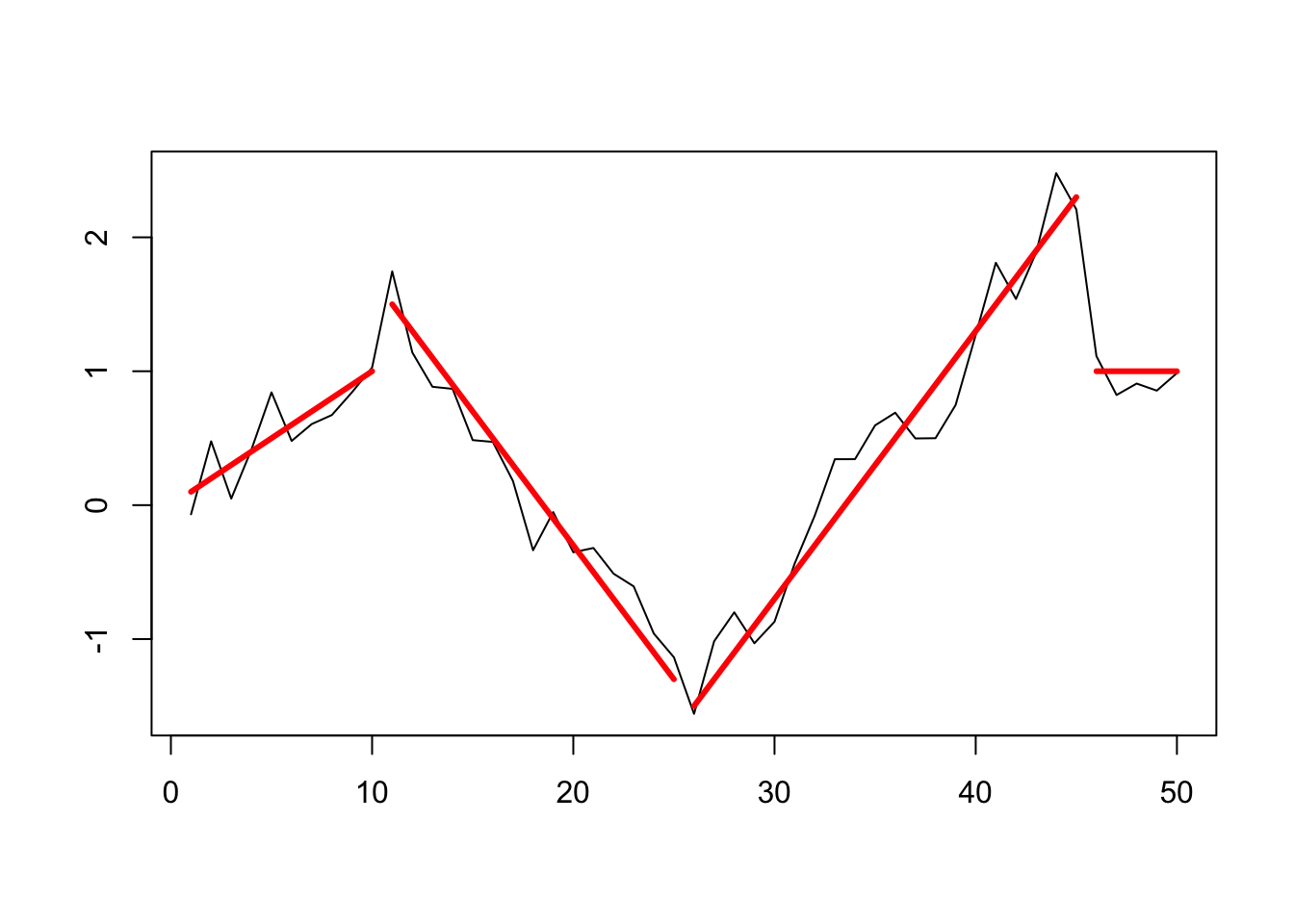
z_ts <- every bit.ts(df$z) (changepoints at ten/xi, 25/26, 45/46)
changepoint
Testing for 1 alter bespeak in mean
## Created Using changepoint version 2.2.ii ## Changepoint type : Change in mean ## Method of analysis : AMOC ## Test Statistic : Normal ## Type of penalty : MBIC with value, 11.73607 ## Minimum Segment Length : ane ## Maximum no. of cpts : 1 ## Changepoint Locations : Nothing establish with the AMOC method.
Testing for several using PELT method and AIC penalty:
## Grade 'cpt' : Changepoint Object ## ~~ : S4 course containing 12 slots with names ## cpttype date version data.set up method test.stat pen.blazon pen.value minseglen cpts ncpts.max param.est ## ## Created on : Fri Apr 26 15:58:35 2019 ## ## summary(.) : ## ---------- ## Created Using changepoint version two.ii.ii ## Changepoint blazon : Change in mean ## Method of analysis : PELT ## Test Statistic : Normal ## Type of penalty : AIC with value, 4 ## Minimum Segment Length : ane ## Maximum no. of cpts : Inf ## Changepoint Locations : 17 32 Testing for several using PELT method and CROPS punishment:
## [one] "Maximum number of runs of algorithm = eight" ## [1] "Completed runs = 2" ## [1] "Completed runs = 3" ## [1] "Completed runs = v" ## [one] "Completed runs = 7" ## Created Using changepoint version two.2.two ## Changepoint type : Change in mean ## Method of analysis : PELT ## Test Statistic : Normal ## Type of penalty : CROPS with value, one 25 ## Minimum Segment Length : 1 ## Maximum no. of cpts : Inf ## Changepoint Locations : ## Number of segmentations recorded: 7 with between 0 and 6 changepoints. ## Punishment value ranges from: 1 to fourteen.97552 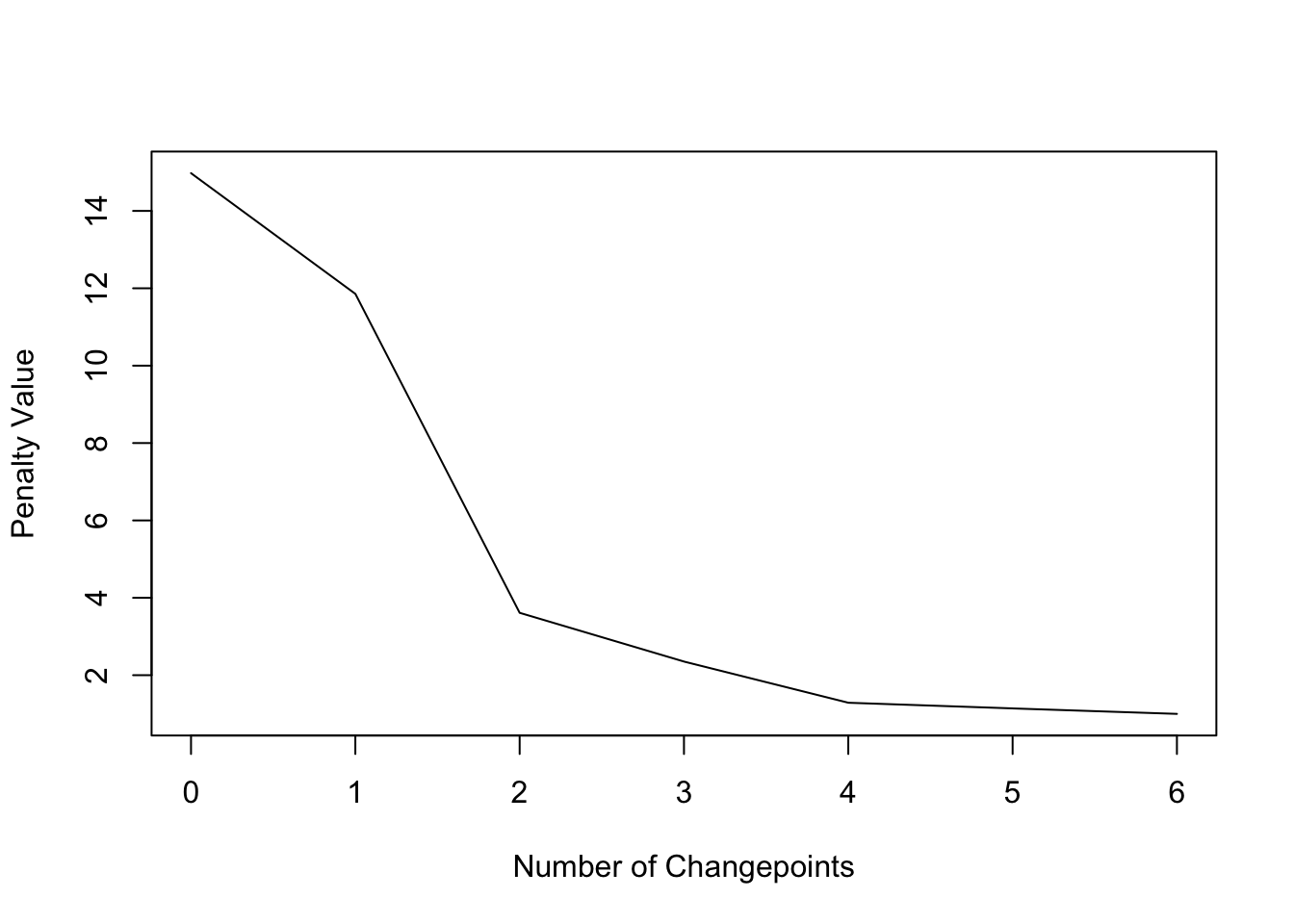
## [,i] [,ii] [,iii] [,4] [,five] [,6] ## [1,] 4 xvi 23 31 39 45 ## [ii,] 17 23 31 39 45 NA ## [3,] 17 31 39 45 NA NA ## [four,] 17 31 39 NA NA NA ## [5,] 17 32 NA NA NA NA ## [six,] 39 NA NA NA NA NA ## [vii,] NA NA NA NA NA NA Changepoints at 17, 31, 39, and 45 detected:
plot(cpt2, ncpts = iv) 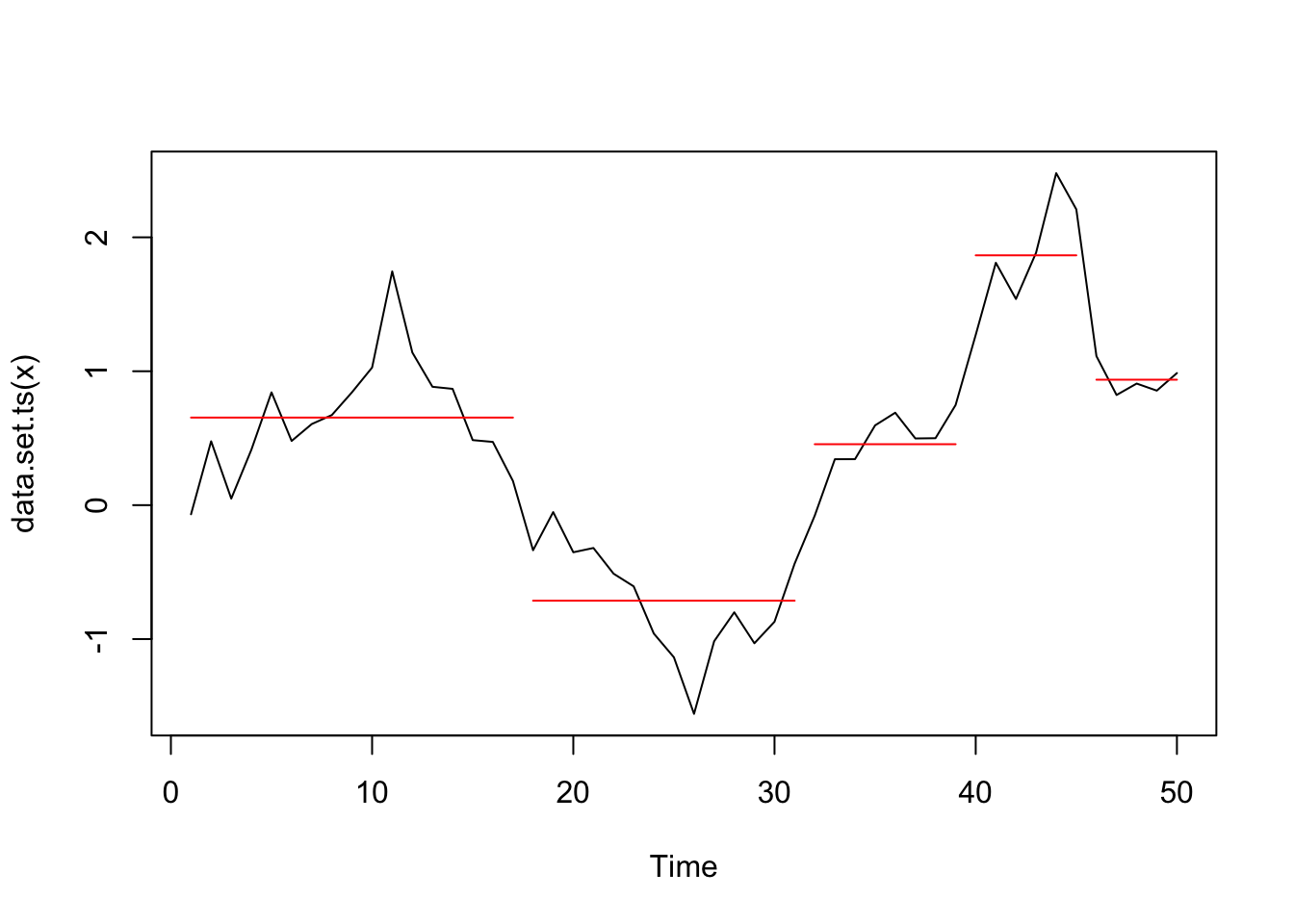
bcp
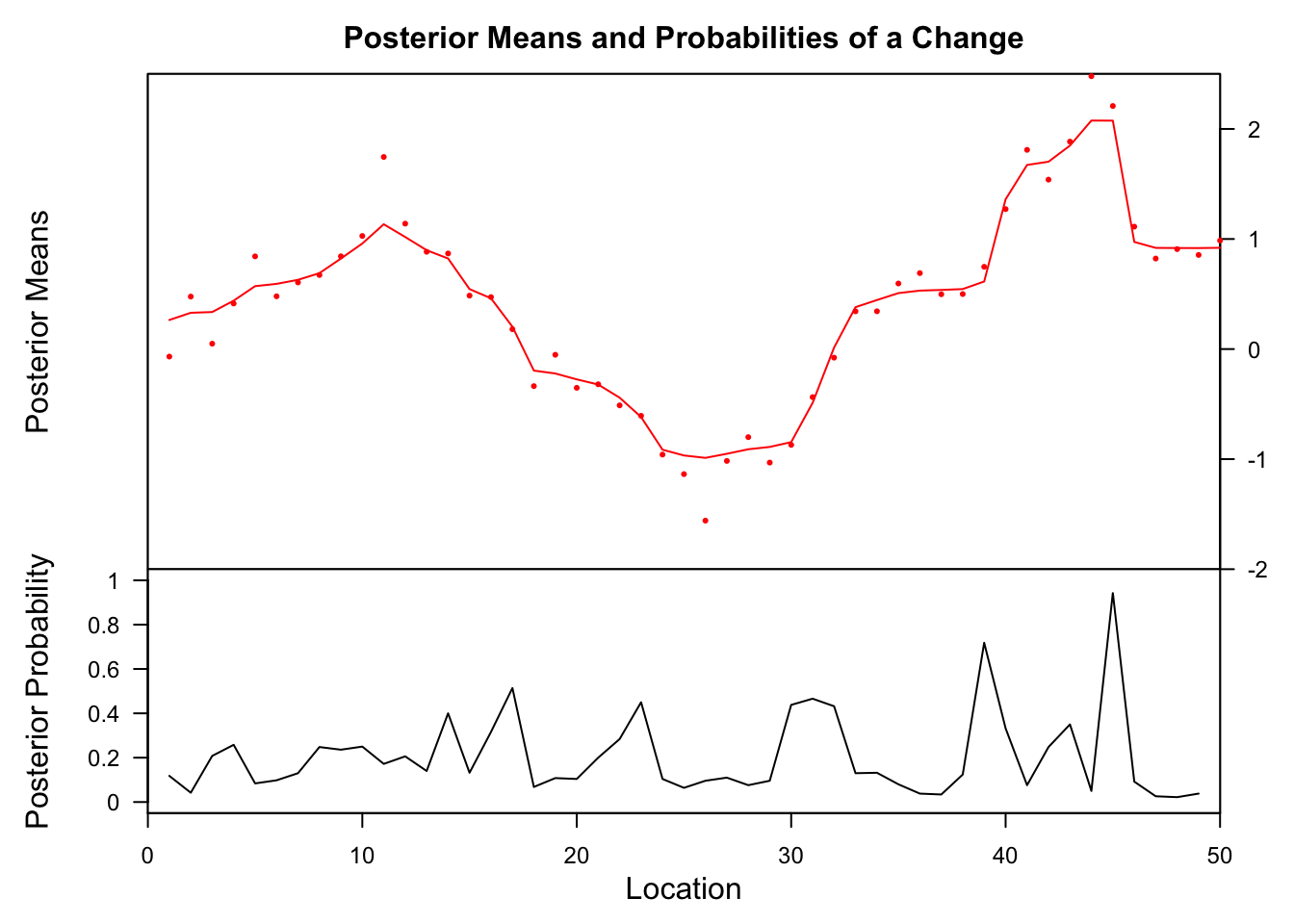
## Probability X1 id ## 39 0.718 0.6137687 39 ## 45 0.942 two.0753858 45 The bcp method finds also at x = 39 and 45 change points but not before.
strucchange
Generalized fluctuation test 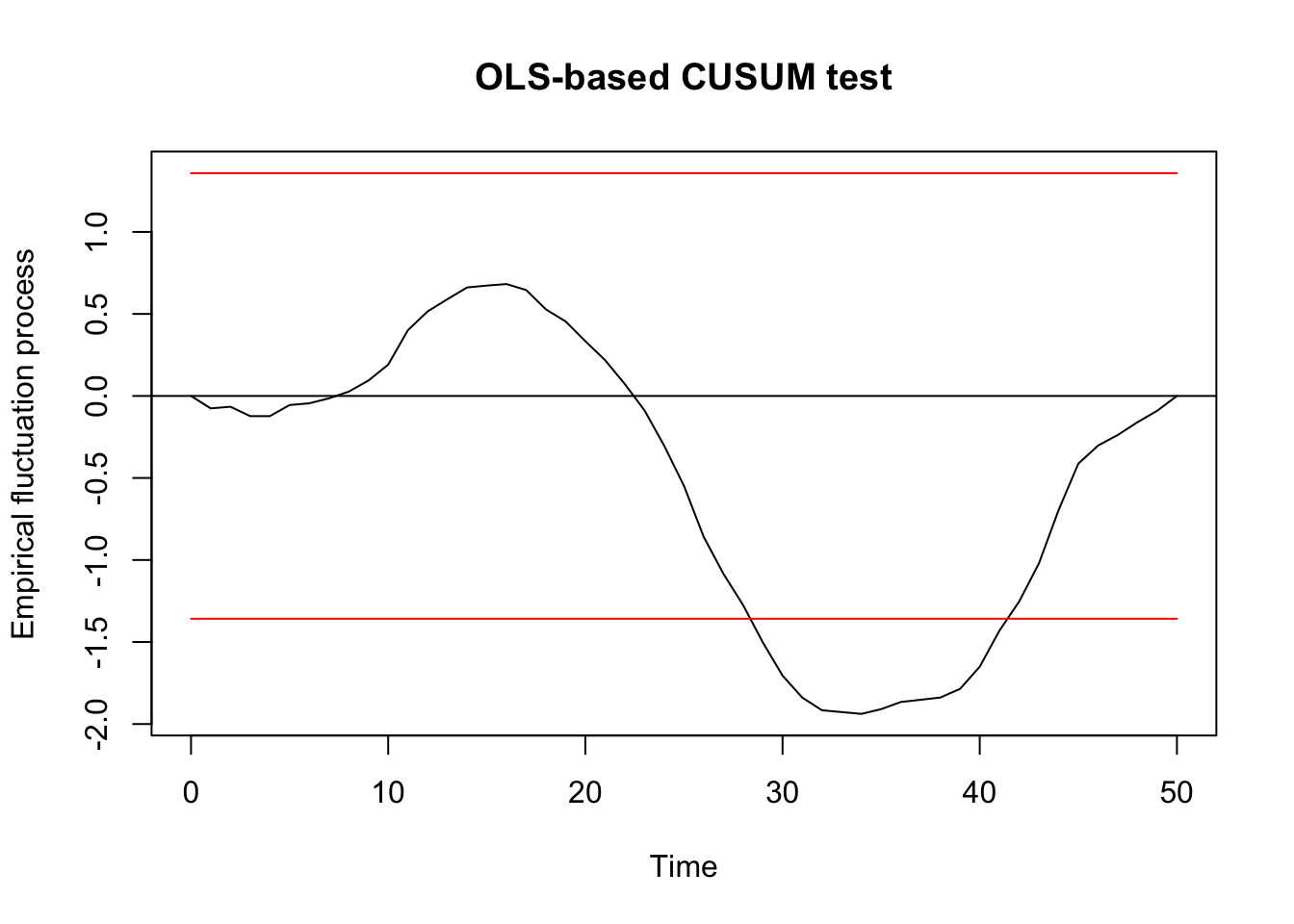
## ## OLS-based CUSUM test ## ## data: ocus_mod ## S0 = 1.9381, p-value = 0.001093 F examination
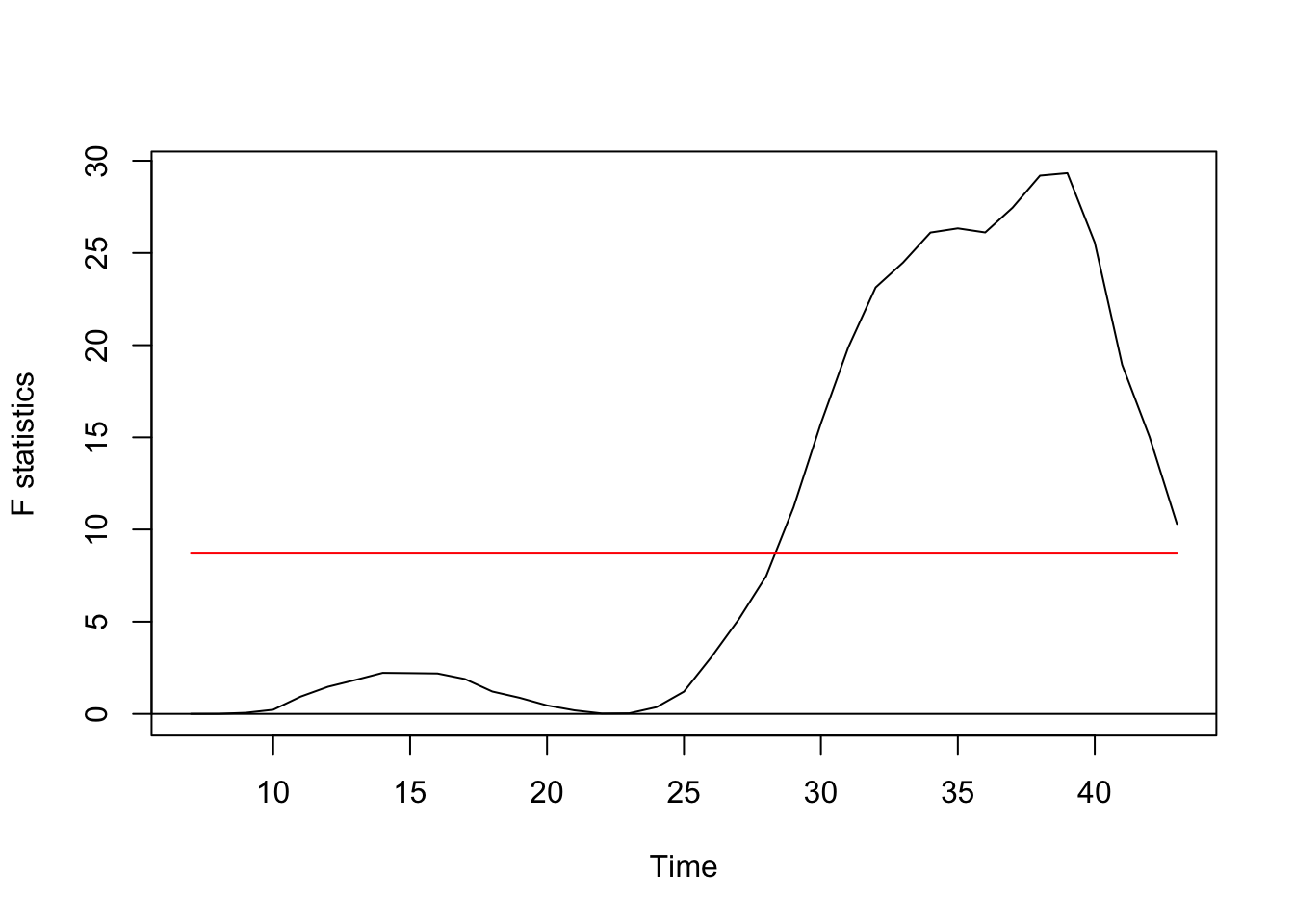
Regression breakpoints
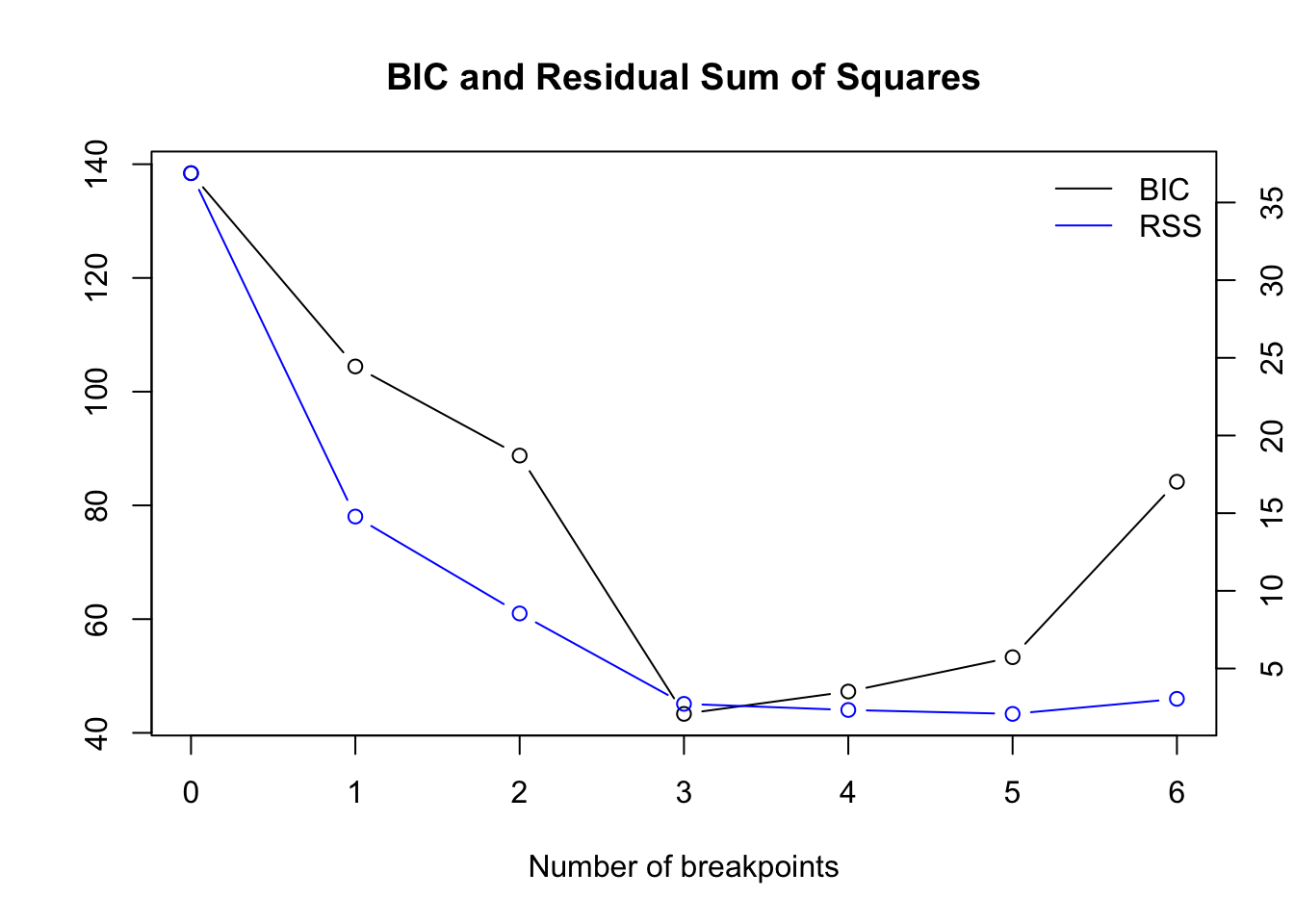
Get the optimal number numerically:
bpts_sum <- summary(bpts) opt_brks <- opt_bpts(bpts_sum$RSS["BIC",]) opt_brks ## [1] 3 Location of breakpoint:
## [ane] 10 26 43 The first 2 approaches in strucchange observe 1 significant alter point while the breakpoints algorithm finds 3:
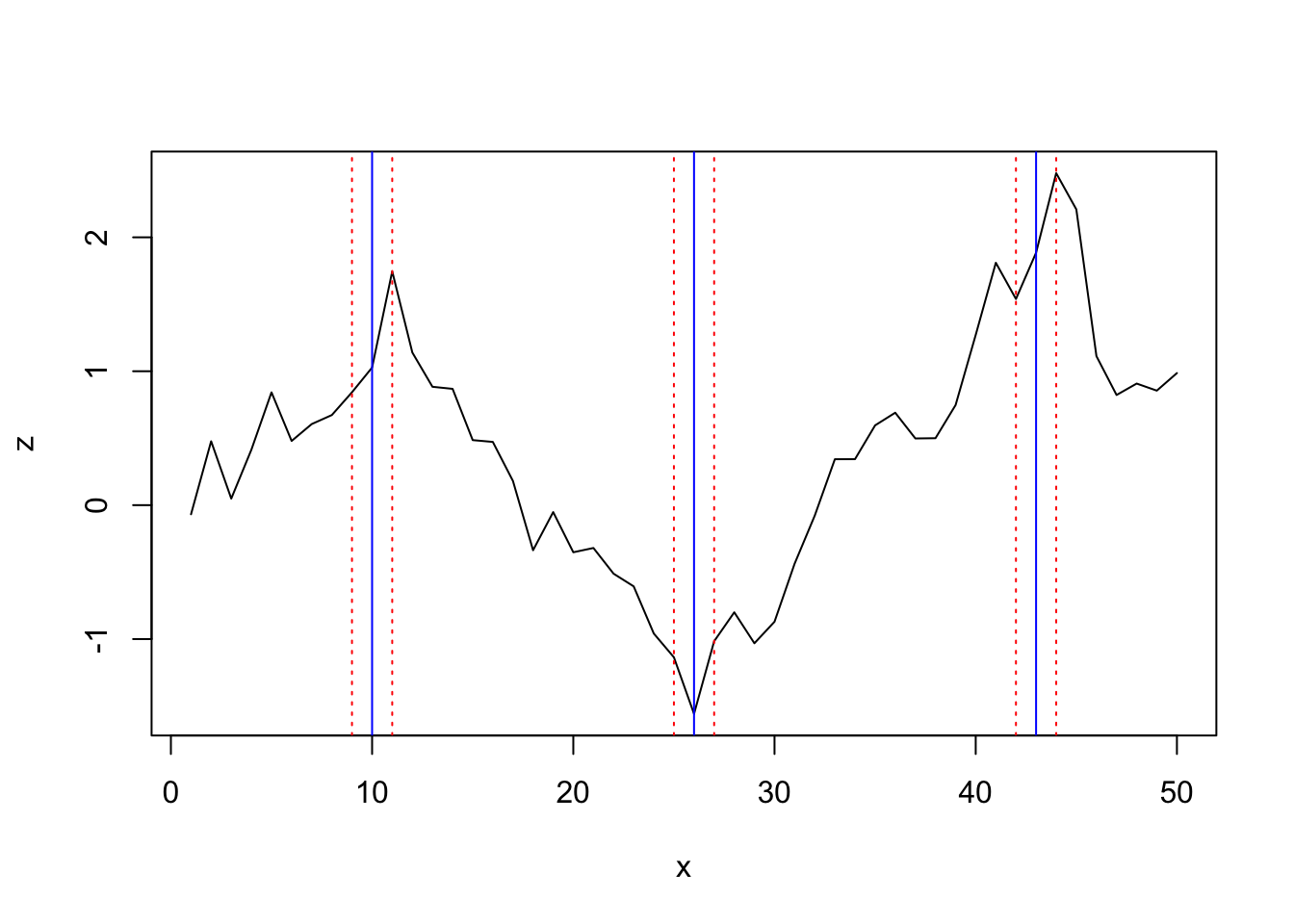
segmented
Since I demand to specify the number of modify points direct in the function and i see already in the z~ten plot several changes I provide 3 starting values (simply for the purpose of functioning evaluation will choose rather dissimilar ones):
lin_mod <- lm(z ~ ten, data = df) segm_mod <- segmented(lin_mod, seg.Z = ~x, psi=list(10=c(five,20,35))) summary(segm_mod)$psi ## Initial Est. St.Err ## psi1.ten 5 xi.02788 0.6905547 ## psi2.x 20 26.00047 0.5059189 ## psi3.x 35 43.99998 0.6284971 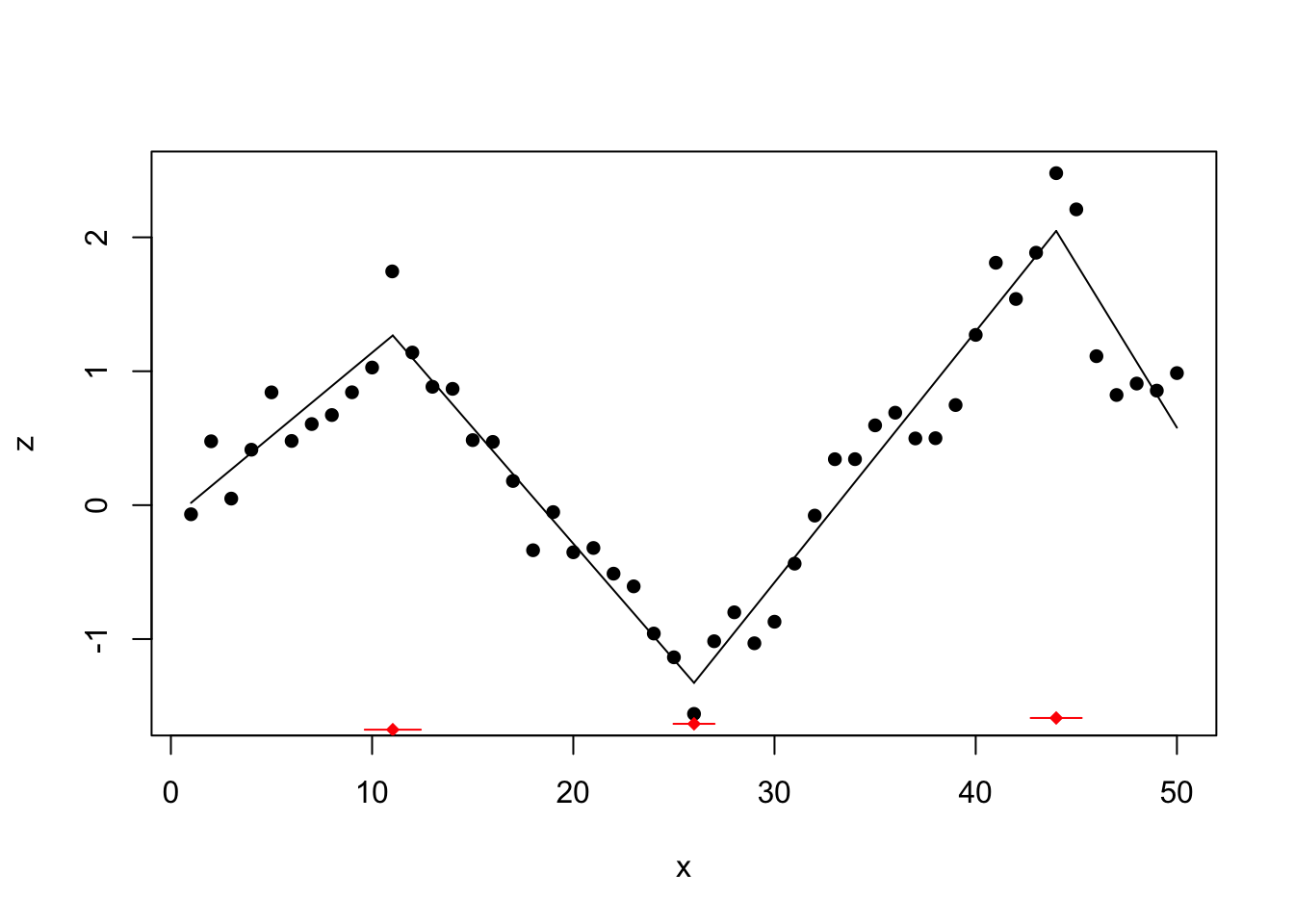
The segmented method finds the 3 change points at location 11, 26, and 44.
tree
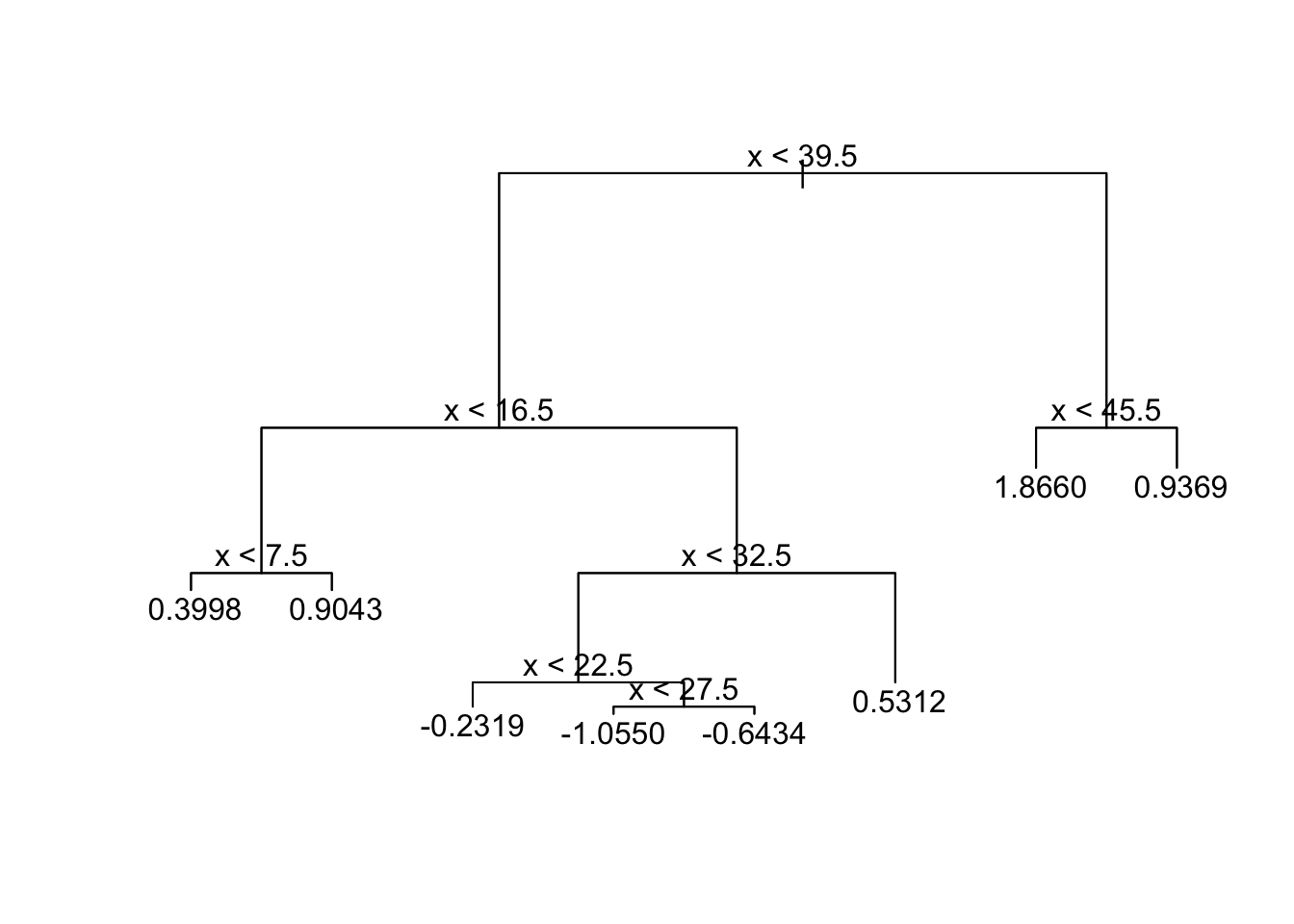
The tree methods finds 4 change points.
Source: https://www.marinedatascience.co/blog/2019/09/28/comparison-of-change-point-detection-methods/
Posted by: bartleytheds1985.blogspot.com


0 Response to "Does A Suppressor Change Point Of Impact"
Post a Comment